Reports: ND953240-ND9: Nonlinear Electrohydrodynamics of Emulsions in Strong Electric Fields
David Saintillan, PhD, University of California San Diego
Motivated by applications in the oil refinement industry based on demulsification by electrocoalescence, the aim of this project has been the development of a combination of detailed numerical simulations and semi-analytical models to systematically study the deformation and dynamics of liquid drops in strong electric fields. Of particular interest here is the so-called Quincke regime, in which recent experiments have demonstrated that emulsions can exhibit symmetry breaking bifurcations and a transition to unsteady chaotic dynamics with large deformations as field strength is increased; these effects, which are likely to impact coalescence and breakup, have not yet been fully explained theoretically nor reproduced in simulations.
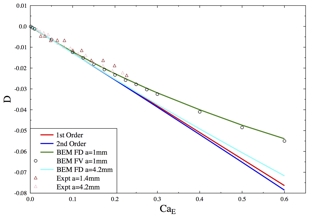
Two different numerical approaches have been developed to address this problem. First, we developed a novel boundary element formulation in both two and three dimensions. The main advantages of using the boundary element method are accuracy and decreased computational time compared to methods based finite elements or finite differences, which require discretization of the entire fluid domain. While boundary element simulations of drops in electric fields had been performed before, such simulations did not include charge convection by the flow, which is an essential aspect of this problem, and were also limited to axisymmetric geometries and were therefore unable to capture symmetry breaking and Quincke electrorotation. The novelty in our work lies in the formulation of a boundary element method for the full Taylor-Melcher leaky dielectric model including unsteady effects and charge convection. Specifically, our method is based on triangular curved elements and uses a semi-implicit scheme in time to enhance stability. An important part of the code development also consisted in devising schemes to treat the singularities that are known to exist in three-dimensional boundary integral formulations. The code was first tested and validated in detail in the small deformation regime by comparison with previous analytical, computational, and experimental data available in the literature, and excellent agreement was found as shown in figure 1.
Figure 1: Drop deformation parameter as a function of electric Capillary number (dimensionless field strength) from linear theories of 1st and 2nd order, boundary element (BEM) simulations, and experiments
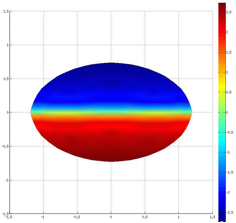
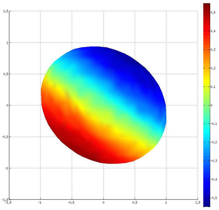
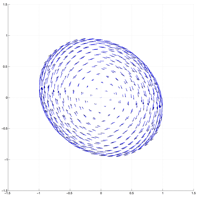
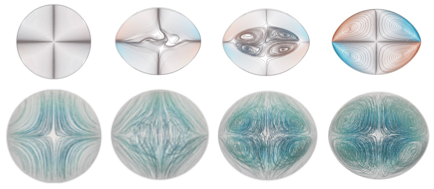
Our efforts then focused on investigating the strong field regime or Quincke regime. Upon increasing field strength, our simulations revealed two novel phenomena. First, we showed that charge convection by the flow on the drop interface can lead to the formation of a charge shock at the drop equator, where a sharp discontinuity is observed in the charge distribution due to the sweeping of opposite charges by the interfacial flow. This shock, which is illustrated in figure 2, is quite challenging to resolve numerically and in the most severe cases led to numerical instabilities. The existence of this shock was further verified by a semi-analytical model for a nearly spherical droplet, which indeed led to a hyperbolic equation with shock solutions for the surface charge distribution. Second, we were able to observe in strong fields the symmetry breaking bifurcation reported in experiments, which leads to destabilization of the axisymmetric configuration and ultimately to a tank-treading regime known as Quincke electrorotation illustrated in figure 3. To our knowledge, these are the first numerical simulations ever to capture this regime. Detailed comparisons with experimental data obtained by other groups showed excellent quantitative agreement for the critical field strength above which such dynamics occur.
Figure 2: Formation of a charge discontinuity at the equator of an oblate drop in a strong electric field.
Figure 3: Quincke electrorotation: Symmetry breaking bifurcation and transition to a tank-treading regime in strong fields. Left panel: charge distribution. Right panel: Interfacial fluid velocity.
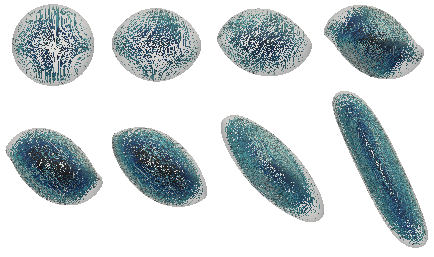
Upon further increasing the electric field, our boundary element simulation code was found to exhibit numerical instabilities, which did not allow us to address the large deformation regime accessible in experiments. As a result, this led us to consider a second different numerical approach to tackle the same problem based on finite elements. To this end, we developed an entirely different numerical method for modeling complex flows of incompressible immiscible fluids with both electric and hydrodynamic effects. In this finite volume method, a level-set is used to describe the interface, allowing both the interface and interfacial continuity equations to be treated in a sharp manner. This approach, which is quite computationally expensive, was implemented on adaptive Octree/Quadtree grids, which are highly effective in capturing the different lengths scales of the problem while minimizing the number of finite volumes. By using a modified pressure correction projection method, we were able to alleviate the standard time step restriction incurred due to viscous forces. The solver was first validated in two and three spatial dimensions on a number of benchmark problems, and was eventually applied to the case of droplets in electric fields. As for the boundary element method, the solver was first tested in the small deformation regime (see figure 4) by comparison to experimental data, and good agreement was found. The Quincke regime was also observed in these simulations, with the additional advantage that the increased stability of the method allowed us to probe large deformations as occur in very strong fields. A typical simulation showing the symmetry breaking bifurcation in the strong deformation regime is shown in figure 5. A detailed analysis of these recent simulations with comparison to existing experimental data is currently underway, with the aim of further elucidating the physical mechanisms leading the destabilization of the axisymmetric shape.
Figure 4: Oblate deformation of a droplet in the small deformation regime, showing the formation of Taylor vortices, in finite volume simulations. Top row: two dimensions. Bottom row: three dimensions.
Figure 5: Time series showing the symmetry breaking bifurcation and transition to Quincke electrorotation in a strong electric field, in the large deformation regime.