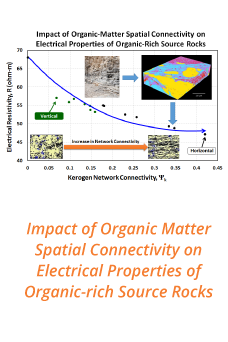
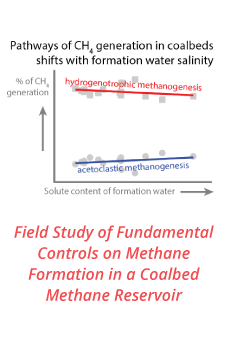
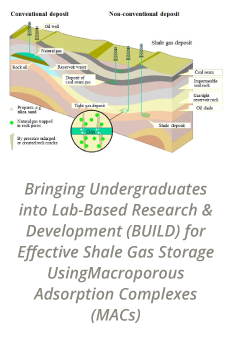
Reports: ND554513-ND5: Mechanics and Stability of Surface-Confined Assemblies
Gregory M. Grason, University of Massachusetts Amherst
Benjamin Davidovitch, University of Massachusetts
This proposal addresses the structure, mechanics and stability of sheet-like, particulate assemblies confined to curved interfaces, a primary example of which is particle-coated fluid interfaces, or Pickering emulsions. This problem remains poorly understood owing to the nontrivial competition between relaxation modes that involve shape deformation of the droplet, rearrangement of the particles, rupture of the sheet, and desorption of particles from the interface. The long-term goal the project is to develop a theoretical framework to place and compare these distinct modes on a single “structural response” phase diagram. A predictive and testable understanding of the interplay between these distinct modes of will facilitate critical improvements to particle-mediated methods for processing complex fluids mixtures.
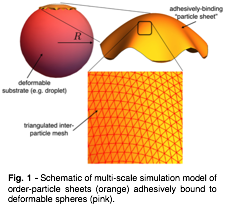
Fig. 1 - Schematic of multi-scale simulation model of order-particle sheets (orange) adhesively bound to deformable spheres (pink).
As a first step towards the long-term goal, a primary aim of the project is to study the structure and energetics of hexagonally-ordered sheets bound to spherical, yet deformable, substrates as a primitive model for capillary-mediated particle assemblies at liquid droplet interfaces. To this end, we are developing a combination of continuum elasticity and coarse-grained simulation approaches to investigate the structure and energetics of competing patterns of wrinkles and lattice dislocations that both relax stresses in circular sheets adhered to deformable sphere. Based on these models, we will relate the particle-sheet morphology to parameters that govern the overall shape and mechanics of the sheet, including the size and effective elasticity of the sheet, and shape, deformability and adhesive strength of the substrate (e.g. droplet), as well as further parameters that control the microscopic sheet behavior, such as bending stiffness and core size and energies of lattice defects. In later stages of the project, the model will be generalized to include the impact of cohesive inter-particle forces in regulating crack-formation and particle-desorption instabilities, as well as variations of surface geometry, including negatively-curved models of inter-droplet “necks”.
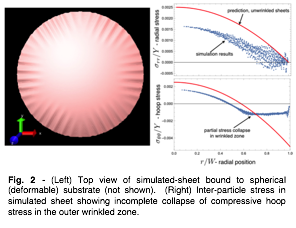
In the first year of this project, our efforts have focused on 1) developing and implementing a coarse-grained simulation model of hexagonally-order sheets bound to deformable spheres; and 2) developing a theoretical understanding of the wrinkling response of finite-thickness sheets bound to spheres in the limit weak adhesion at the sheet edge. For the first aim, we have implemented numerical model of triangulated bond network (Fig. 1), to model stretchable cohesive inter-particle bonds, bound to a sphere with a solid-like elastic response which also acts to generate a lateral (in-plane) tension in the sheet through the adhesive sheet/substrate interaction which favors spreading of the assembly over the sphere (Fig. 1). Our first exploration of this model focuses on the wrinkling response of sheet, and in particular, the structure of radial wrinkle patterns forming in the sheet in the uncharacterized limit where tensile boundary forces are small compared to out-of-plane bending stiffness of the sheet (typically associated with thickness of an elastic layer). In the opposite limit, studied previously and applied to experimental studies of stressed, amorphous polymer films, where sheets are sufficiently bendable, the size of the wrinkled zone is shown to be governed predominantly by the adhesive boundary forces with the substrate. Here, our numerical simulations have uncovered a new regime where the finite bending stiffness of the membrane limits the amount of stable compression allowed in the wrinkle zone, and thereby, leads to a relation between the length of wrinkles and the geometric mean of bending stiffness of the sheet and modulus of the substrate (Fig. 2). We have a developed and numerically tested a new scaling relation between wrinkle-length and sheet stiffness, and are currently developing analytical approaches to the crossover behavior between tension-governed, and bending stiffness-governed wrinkling. In the next phase of the project, currently underway, we are developing and implementing a method to introduce and relax the position of lattice dislocations in the sheet. This will provide the first numerical test of preliminary predictions of a transition between wrinkled-mediated relaxation to defect-mediated relaxation in ordered sheets driven either by increasing substrate stiffness or curvature.
Fig. 2 - (Left) Top view of simulated-sheet bound to spherical (deformable) substrate (not shown). (Right) Inter-particle stress in simulated sheet showing incomplete collapse of compressive hoop stress in the outer wrinkled zone.
The project involves the training of a Physics Ph.D. graduate student who is jointly advised by PIs Grason (Polymer Science and Engineering) and Davidovitch (Physics). Through this interdisciplinary research project, this student will learn a combination of techniques for soft materials modeling, including elasticity theory and geometry of crystalline sheets and numerical simulation methods for multi-scale structures. This project involves a collaboration with Prof. Rastko Sknepnek (University of Dundee) to develop new algorithms for physical processes of multi-scale structure relaxation in deformable membranes, to be ultimately incorporated into and distributed through a simulation package he is developing.