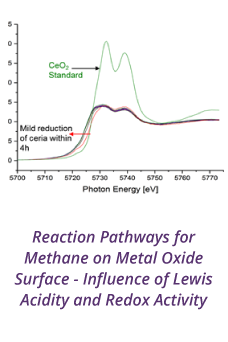
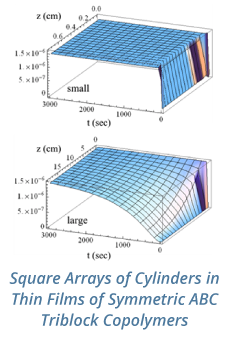
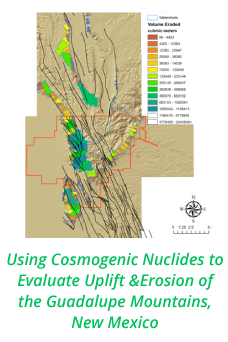
Reports: DNI952295-DNI9: Multi-Scale Investigation of Viscoelastic Micellar Fluids in Complex Flows
Matthew E. Helgeson, PhD, University of California (Santa Barbara)
Summary. We seek a thorough understanding of flows of wormlike micelles (WLMs) in realistic processing flows. In FY2013, we identified that complex drag flows were dominated by the emergence of highly localized shear bands near the moving surfaces, suggesting that complex flows of WLMs are dominated by shear banding. To better understand this coupling, work in FY2014 focused on studying how curvature impacts the development of shear banding in wide-gap Taylor-Couette flow, including both experiments and modeling using the Vasquez-McKinley-Cook (VCM) constitutive model. We found that increasing curvature leads to an expansion of the envelope of critical shear rates for banding, and that the onset of shear banding occurs when the local shear rate exceeds a curvature-independent threshold. For complex flows, this leads to the formation of a narrow high-shear band near no-slip boundaries, thereby creating effective slip in the remaining flow.
These results suggest that constitutive models that predict critical shear rates for shear banding are essential to understanding WLMs in complex flows. In FY2015, we therefore interrogated of the only constitutive model that incorporates the physics of reversible chain scission for WLMs – the VCM model. Using rheological and neutron scattering measurements, we developed a model system containing linear WLMs, independently measured parameters of the VCM model as a function of the average micellar length, and tested model predictions against velocimetry measurements over a range of conditions. We find that the model makes poor predictions when using independently measured parameters, and furthermore gives unphysical values for these parameters when used as a fitting model to the velocimetry data. We attribute these inadequacies primarily to the way in which the model coarse-grains the length distribution of micelles. Ongoing studies are aimed at measuring the equilibrium and non-equilibrium length distributions of micelles over a wide range of conditions, and using them to formulate models with that more accurately capture the kinetics of micelle breakage.
Having uncovered the critical role of micellar breakage and length distribution in determining when (and where) shear banding occurs in complex flows, we ultimately seek to make measurements of how flow-induced micellar scission and reformation are impacted by complex deformation fields. Toward this end, we have prototyped a new flow cell based on the concept of a “microfluidic four-roll mill” with collaborators at NIST to enable such measurements using flow-SANS. In the past year, the PI received an Early Career Award from the Department of Energy Basic Energy Science – Neutron Scattering program, which will fund the continuation of this work.
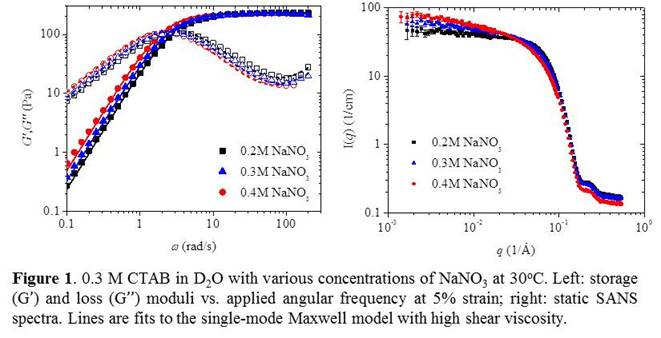
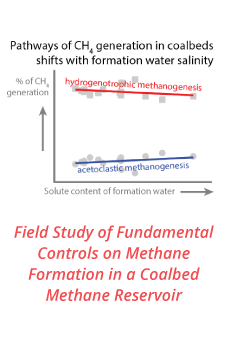
Detailed progress. To study effect of chain scission and reformation on shear banding of WLMs and validate the VCM model, we chose a series of 0.3 M cetyltrimethylammonium bromide (CTAB) in D2O with various concentration of sodium nitrate (NaNO3), producing a series of micelles with varying average length at constant total micelle concentration. Linear viscoelasticity measurements (Figure 1 left) suggest the presence of linear micelles, since the plateau modulus (G0) remains constant and the relaxation time (λ) increases monotonically with increasing salt concentration. This is confirmed by SANS spectra at equilibrium (Figure 1 right), I(q), due to the observed increase in I(0).
Rheological
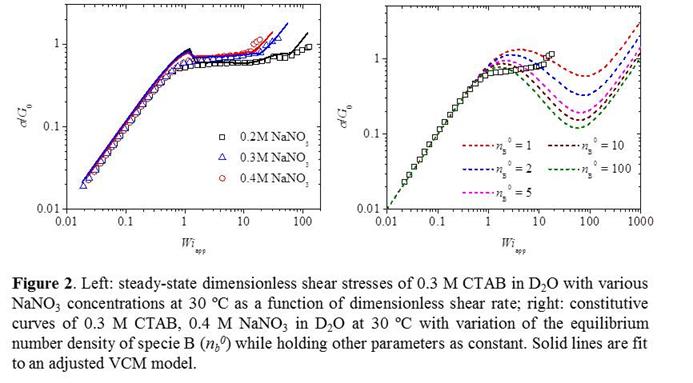
measurements (Figure 2 left) suggest all three of the samples to be shear
banding. The shear stresses (σ) are non-dimensionalized by G0
and plotted as a function of dimensionless apparent shear rate ![]() ,
where
,
where ![]() is the applied
shear rate. Banding begins above a lower critical shear rate (Wic1)
and ends beyond an upper critical shear rate (Wic2). Although
Wic1 ~ 1 for all three samples, Wic2
decreases significantly with increasing average micelle length.
is the applied
shear rate. Banding begins above a lower critical shear rate (Wic1)
and ends beyond an upper critical shear rate (Wic2). Although
Wic1 ~ 1 for all three samples, Wic2
decreases significantly with increasing average micelle length.
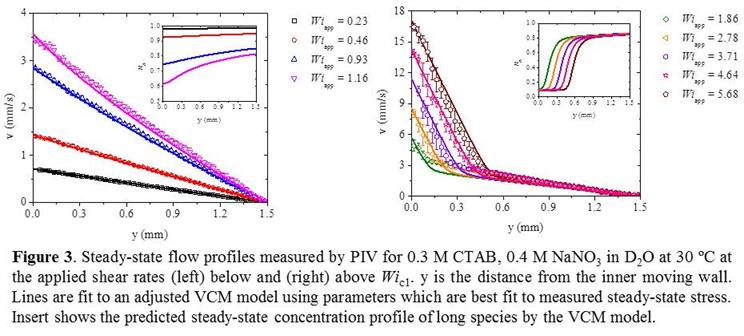
VCM model parameters were obtained as described previously.1,2,3 Using these parameters, the model fails to predict the steady-state flow curve (Figure 2 right, dotted lines), primarily due to an inability for the VCM model to capture the correct high-shear viscosity. Because the model coarse-grains the length distribution into a long species that breaks under shear to produce two short species of half-length, this implies that it underpredicts the amount of the latter produced by scission of the former. We therefore simply used the VCM model as a fitting tool to the rheological or kinematic measurements (Figures 2 and 3). However, this produces values for the relative equilibrium concentration of short species, nb0, which increase with NaNO3 concentration (not shown). This result is unphysical and inconsistent with equilibrium measurements which clearly show an increase in micellar length with increasing concentration. We therefore conclude that, at the very least, a more realistic coarse-graining of the length distribution is needed in the VCM model. To do so, we have made flow-SANS measurements, analysis of which is ongoing.
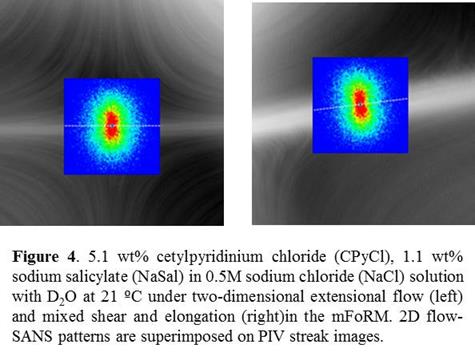
Finally, as mentioned above, we have developed a prototype millifluidic four roll mill (mFoRM), and used it to make preliminary in-situ kinematic and structural characterization of WLMs under two-dimensional complex flows (Figure 4). Specifically, we have made measurements at identical Wiapp for flows approximating 2D elongation (left) and mixture of shear and elongation uniform 2D (right). Interestingly, the 2D SANS pattern exhibits greater segmental anisotropy of micelles in the mixed flow case, a completely novel and unexpected result. Clearly, these preliminary measurements warrant further studies on how the dynamics of WLMs are altered by the type of deformation encountered.
References
1. Vasquez et al., J. Non-Newtonian Fluid Mech. 2007, 144, 122.
2. Pipe et al., J. Rheol. 2010, 54, 881.
3. Zhou et al., J. Non-Newtonian Fluid Mech. 2014, 211, 70.
4. Dunlap & Leal, J. Non-Newtonian Fluid Mech. 1987, 23, 5.