60th Annual Report on Research 2015

The Final Report addresses three achievements:

1.     Engineering the lubrication properties of nanodiamonds with doping:

The current work (see [1]) determines the effects of n-type (replacing an exterior carbon with electron donating nitrogen and oxygen atoms) and p-type (electron withdrawing boron and phosphorus atoms) doping of the adamantane diamond on the chemical potential and chemical hardness. An additional focus is on the performance of HF and a variety of density functionals, including local density approximation (LDA), generalized gradient approximation (GGA), hybrid GGA, meta-GGA and hybrid meta-GGA functionals, for the calculation of the chemical potential and absolute hardness of n- and p-doped adamantane derivatives relative to the high-accuracy diffusion Monte Carlo (DMC) method.

Chemical potential and chemical hardness (Equations 1a and 1b, respectively) are the primary molecular properties used to predict the ability of a material to lubricate. The chemical potential (m) and hardness (h) of a molecular lubricant are usually approximated in terms of the ionization potential (IP) and electron affinity (EA):

Table 1 includes diamondoid electron affinities, ionization potentials, chemical potentials and chemical hardness relative to DMC as calculated with equations 1a, 1b for HF, various DFT functionals and DMC.

The DMC method predicts that all heteroatom doped adamantane systems exhibit a decrease in the chemical hardness and an increase in the chemical potential relative to undoped adamantane.  The largest changes in both properties are observed with the N-doped derivative, providing a 38% decrease in the chemical hardness and a 38% increase in the chemical potential. Doping adamantane has been shown to significantly decrease the band-gap, which is consistent with the observed decrease in chemical hardness observed in this work. 

2. Ground and excited states by the combined Quantum Monte Carlo - Effective Fragment Molecular Orbital (QMC-EFMO) method

The example of an acetone molecule in the presence of four water molecules is used to examine the newly developed QMC-EFMO method for both the ground and excited states [2].

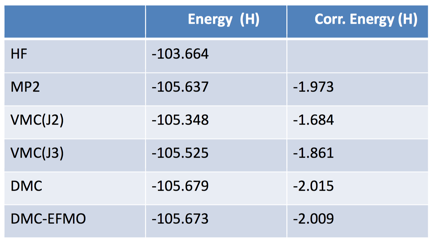
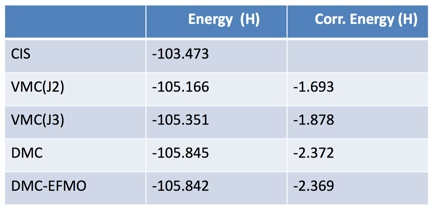
Tables II, III present the ground and first excited state energies respectively of the acetone-four-water system by different high-quality quantum chemical methods: Moller-Plesset second-order perturbation theory (MP2), variational Monte Carlo (VMC) with optimized two-body (J2) and three-body (J3) Jastrow terms, diffusion Monte Carlo (DMC) and DMC-EFMO.

Table II. Acetone and four water molecules (ground state).

Table III. Acetone and four water molecules (first excited state).

3. Mathematical proof of the fixed-node variational principle used in the Quantum Monte Carlo method for the calculation of excited states

A minimum principle for excited states, an alternative to the traditional one based on orthogonality constraints, was proven:

where E_k is the k-th eigenvalue, i.e. the (k-1)-th excited state, and

is a trial wavefunction having the exact nodes of the k-th eigenfunction 

and

is the standard electronic hamiltonian in the Born-Oppenheimer approximation.

Although such a minimum principle for excited states is presupposed in the current practice of QMC, it has never been proven previously, for QMC or for any other quantum mechanics method. The proof does not rely on any specifics of the QMC method; thus, it is of general validity in quantum mechanics. In addition to the proof in principle, an explicit expression for the variation around a given excited state with the nodes constrained to the correct ones was discovered. It is expected that the excited state minimum principle in Eq. (2), presented in more details in the forthcoming publication [3], will have a wide range of applications due to the general validity of the minimum principle for excited states.

[1] A. Findlater, F. Zahariev, and M. S. Gordon, Engineering nanodiamond lubrication properties by doping: A DFT and QMC comparison, (in preparation for publication).

[2] F. Zahariev, A. Findlater, and M. S. Gordon, Ground and excited state by the combined Quantum Monte Carlo - Effective Fragment Molecular Orbital (QMC-EFMO) method, (oral presentation at the 249th ACS National Meeting & Exposition March 22-26, 2015 in Denver, Colorado; in preparation for publication).

[3] F. Zahariev, M. S. Gordon, and M. Levy, Minimum principle for excited states by constraining the nodes only, (in preparation for publication in Phys. Rev. X).

Impact on Careers of Particpants

Three researchers have participated in this work:

1.  Alex Findlater, graduate student. Mr. Findlater, an extremely talented student, has done nearly all of the calculations that are reported here. In the process, he has become an expert in both the quantum Monte Carlo (QMC) method and the interface between QMC and our effective fragment molecular orbital (EFMO) method. At least two publications will eventuate from this work, one of which is in draft form. These papers will appear as chapters in his PhD thesis, which is expected to be completed by the summer of 2016. Mr. Findlater has been encouraged by both Argonne National Laboratory and Pacific Northwest National Laboratory to apply for postdoctoral research appointments. It is very likely that he will be employed by one of these eminent National Laboratories when he completes his PhD. The PRF ND grant has played a major role in Mr. Findlater's progress toward his PhD.

2. Federico Zahariev, Assistant Scientist. Dr. Zahariev, a highly innovative scientist, worked with Mr. Findlater to develop the QMC capability and the QMC-EFMO interface. Dr. Zahariev in very large part conceived of the QMC component of this effort. In addition, Dr. Zahariev played the lead role in the development of the fixed node variational principle, together with our colleague Professor Mel Levy. Because of his efforts, Dr. Zahariev has been nominated for promotion to Associate Scientist.

3. Mark Gordon, Distinguished Professor, PI. The PRF ND grant has enabled Professor Gordon, together with Mr. Findlater and Dr. Zahariev, to explore new directions in the application of QMC theory to novel problems, such as the structure and properties of nanodiamonds. The interface of QMC with the EFMO method, developed in the Gordon group is especially important since it greatly expands the sizes of systems that can be studied with high levels of theory. This effort has greatly enhanced the Gordon group research effort.