60th Annual Report on Research 2015

Introduction

In this study, we are interested to model, at the pore scale, the exchange of stresses and energy between a fluid and its porous host under various conditions. In the first half of our study (last year's report), with a PhD student Yanqing Su, we focused on the transmission of dynamical stresses in the pore fluid and the effect of frequency over the dynamical response of the saturated porous media (Huber and Su, Geofluids, 2015). This year, another PhD student Hamid Karani and I focused our attention to heat transfer and considered the common case where the fluid and solid thermal properties are not identical.

Results

We proposed a new approach for studying conjugate heat transfer using the lattice Boltzmann method (LBM). The approach is based on reformulating the lattice Boltzmann equation for solving the conservative form of the energy equation. This leads to the appearance of a source term, which introduces jump conditions at the interface between different thermal properties. The proposed source term formulation conserves both conductive and advective heat flux (this paper is published, Karani and Huber, Physical Review E, 2015). The model is tested against several benchmark problems including steady-state convection-diffusion within two fluid layers (see Figs. 1 and 2), unsteady conduction in a three-layer stratified domain and steady conduction in a two-layer annulus. The LBM results are in excellent agreement with analytical solution.

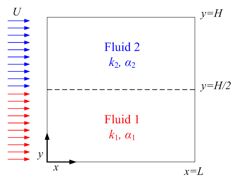
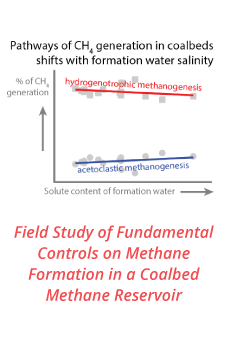
Fig 1. Schematic of 2D convective channel with horizontal interface, from Karani and Huber (2015)

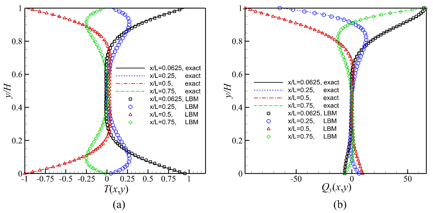
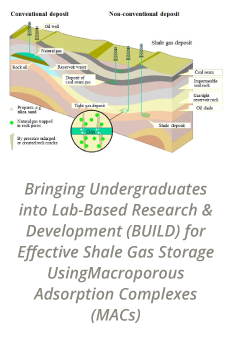
Fig. 2. Comparison of LBM with the analytical solution: (a) temperature, (b) vertical heat flux, for H=L=1, L/Δx=60, k₂/k₁=10, α₂/α₁=1.0 and τ₁=τ₂=0.75, from Karani and Huber (2015)

We further applied the model to natural convection in a porous enclosure (Figs. 3 and 4). The results confirm the reliability of the model in simulating complex coupled fluid and thermal dynamics in complex geometries and retrieves the well-established scaling between the heat transfer parameterized with the Nusselt number and the ratio of thermal buoyancy to flow resistance (Rayleigh-Darcy number) for cases where the thermal conductivity ratio between fluid and solid is 1.

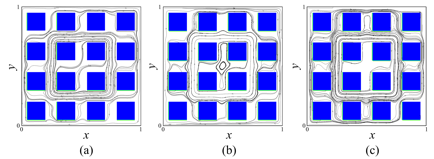
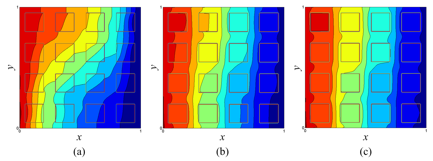
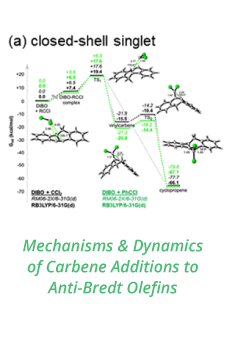
Fig. 3. Streamlines for Ra=10⁵: (a) k_s/k_f=0.1, (b) k_s/k_f=10, (c) k_s/k_f=100 from Karani and Huber (2015).

 Fig. 4.  Isotherms for Ra=10⁵: (a) k_s/k_f=0.1, (b) k_s/k_f=10, (c) k_s/k_f=100, from Karani and Huber (2015).

We are now using this pore-scale model for heat and fluid flow in porous media to study natural convection and the effect of thermo-physical properties on the onset of thermal convection and volume averaged heat transfer efficiency (Nusselt number) in porous media. We find that standard continuum approaches to the thermal energy equation, such as Local Thermal Equilibrium (LTE) or even Local Thermal Non-Equilibrium (LTNE) models fail to reproduce some of the most basic characteristics of natural thermal convection and that new upscaling approaches that explicitly account for microstructural effects, through multiscale representations for example, are required to overcome these issues. We are currently addressing these issues.