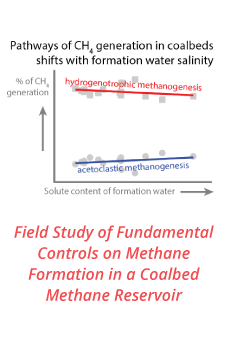
Reports: ND952177-ND9: Direct Numerical Simulation and Experiment of Gas-Liquid Flow in Horizontal Pipelines: A New Approach
Marcus Herrmann, DEng, Arizona State University
Kangping Chen, PhD, Arizona State University
This report outlines progress made in the reporting period; more specifically, the development of a new outflow boundary condition and its implementation for multiphase internal flows.
Development of a new outflow boundary condition for multiphase internal flows
For spatially developing multiphase pipe flows, the physical problem can encompass a large domain while numerical simulations can only focus on a specific section of the system due to finite computational resources. A bounded computational domain for a spatially developing flow presents the technical challenge of imposing proper boundary conditions on the outflow boundary, as the flow variables on such a boundary are generally unknown, and they must be computed in such a manner that the resulting flow field yields both stability and accuracy whilst not causing an unphysical effect on the internal flow field. For single-phase incompressible flows, there have been several outflow boundary treatments in terms of specific spatial discretization (spectral elements, finite elements, etc.) which can maintain numerical stability and physical truthiness even when reversed flow is present at the outflow boundary [1]. There are, however, limited works on multi-phase outflow boundary conditions.
Two promising outflow boundary conditions for multiphase flow have been proposed: zero-flux for the outflow using a coupled level-set/volume-of-fluid method [2]; and energy balance using a spectral-element discretization in conjunction with a phase-field method [3]. The pressure boundary condition that results from the energy balance is handled with a rotational pressure-correction. The work developed in both [1] and [3] show increasing numerical stability with increasing truncated domains, single-phase and multi-phase respectively, when energy influx is present at the outflow boundary. We have adopted the energy balance strategy to develop a numerically-stable multi-phase outflow boundary condition for the Poisson equation using finite-volume spatial discretization in conjunction with an incremental-pressure fractional-step correction algorithm. To track the phase interface, a consistent-rescaled momentum transport [4] is used in conjunction with the refined level-set grid method [5].
The performance and capabilities of the new outflow boundary treatment have been tested in several case studies. The boundary condition has been tested in truncated domains using two and three dimensional problems. The spatial accuracy of the boundary condition has been first tested using a single-fluid problem with known solutions that involve outflow boundaries, showing the effect of truncating the domain on the velocity field. Second, the steady-state flow in a bifurcated channel has been analyzed. These two cases are two-dimensional tests for the single phase capabilities of the boundary condition. The third case involves a two-dimensional droplet moving through an outflow boundary. These tests have demonstrated the robustness of the proposed algorithm. In particular, a convecting drop with a density ratio of 10, 000 is able to move through the outflow boundary with minimal deformation. This is not achievable with any standard outflow treatment. Due to page limitation, the details of these results are not listed here.
Slug generation and discharge in a two-phase channel flow
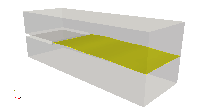
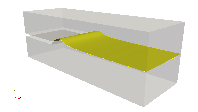
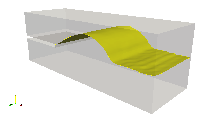
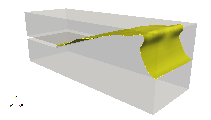
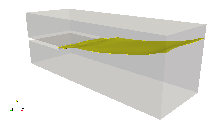
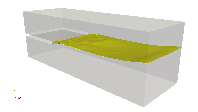
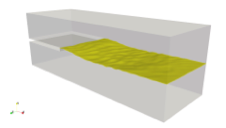
A three-dimensional multi-phase channel flow is used to test the stability of the new outflow boundary condition in internal multiphase flows with high-shear rate, high density-ratio and high viscosity ratio in truncated domains. The simulation mimics water-air flow, with the slow moving heavy and more viscous fluid below a splitter plate and the fast moving lighter and less viscous fluid above the splitter plate prior to mixing. The density ratio is 1,000 and viscosity ratio is 100. A single slug is generated and expelled through the flow domain, with the flow eventually reaching a statistically-steady state. This problem is numerically challenging not only at the outflow boundary, but also in the entire domain, since high-shear and heavily-reversed flow regions are present throughout the simulation. Simulations are performed for two grid sizes, and two domain sizes (length-to-gap ratio of 3, and 9). The two grid sizes show similar results and the larger domain does contain slightly more energy than the short domains, but the differences are tolerable as long as numerical stability is gained. The results are shown in Fig. 1.
Figure 1: Simulation of two-phase channel flow: startup, buildup and discharge of a slug. Time increases from left to right, and top to bottom.
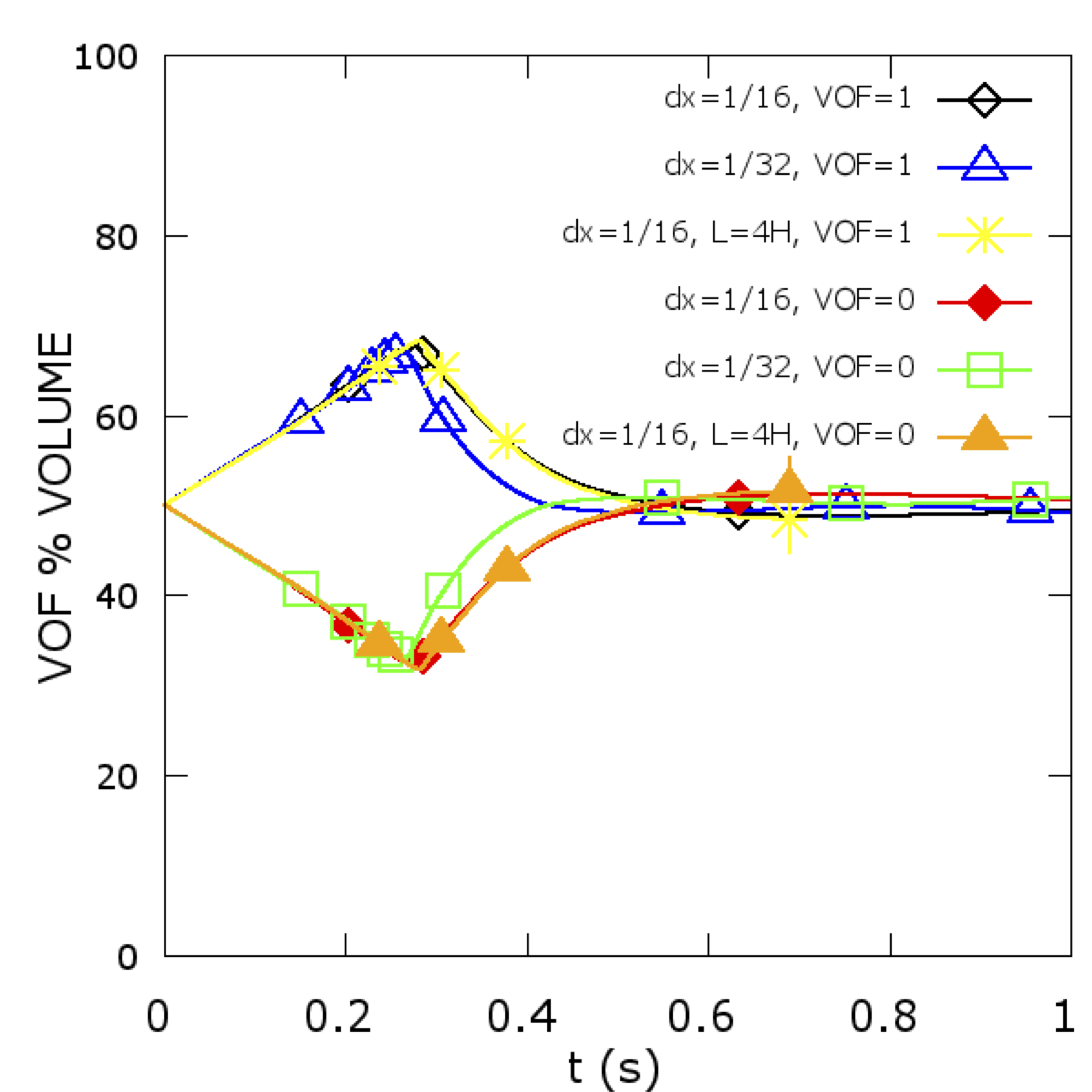
Another important parameter for pipeline flow is the liquid holdup ratio, which is the percentage of the heavy fluid present in the domain at a particular time. For this channel case, the liquid holdup ratio as a function of time is shown in Fig. 2. The heavy fluid initially gains volume in the domain when the slug is forming; then it is slowly reverted to its initial value. The amount of volume of each phase is consistent from the short to large domain.
Figure 2. Percentage of volume occupied by each fluid at a particular time instance.
Applicability of the algorithm
The strategy developed and implemented for the outflow boundary condition for multi-phase flow can be direct applied to a large number of multi-phase flow problems, internal and external, and the implementation to existing code infrastructure is relatively simple. The developed open outflow boundary condition can also be implemented with any interface-transport model that utilizes a fractional step method to solve the governing equations. Although in the current implementation a hybrid of volume-of-fluid/level-set method is used, the method can be implemented with purely volume-of-fluid or with level-set methods on their own. The method presented provides increased numerical stability when kinetic energy influx is present at the outflow boundary. For many applications, it provides a path for simulations which would otherwise not be possible with a standard outflow boundary treatment.
Reference
[1] S. Dong, G. E. Karniadakis, and C. Chryssostomidis. J. Comput. Phys., 261:83-105, March 2014.
[2] A. Albadawi, D.B. Donoghue, A.J. Robinson, D.B. Murray, and Y.M.C. Delaur. International Journal of Multiphase Flow, 53:11-28, 2013.
[3] X. Wang S. Dong. Dec 2014. arxiv.org/pdf/1412.8735. arxiv.
[4] S Ghods and M Herrmann. Physica Scripta, 2013(T155):014050, 2013.
[5] M. Herrmann. Journal of Computational Physics, 227(4):2674-2706, Feb 2008.