60th Annual Report on Research 2015

This research project has two major goals: the development of computational methods for the characterization of intermediates in electron-induced reactions and the characterization of these intermediates themselves. During the third year two projects begun in year two were finalized. The investigation of extrapolation methods yielding energies and lifetimes was concluded and published, and a new class of absorbing potentials wrapping perfectly around molecular systems–very much like van der Waals surfaces–were studied and applied to a number of smaller and intermediate size molecules.

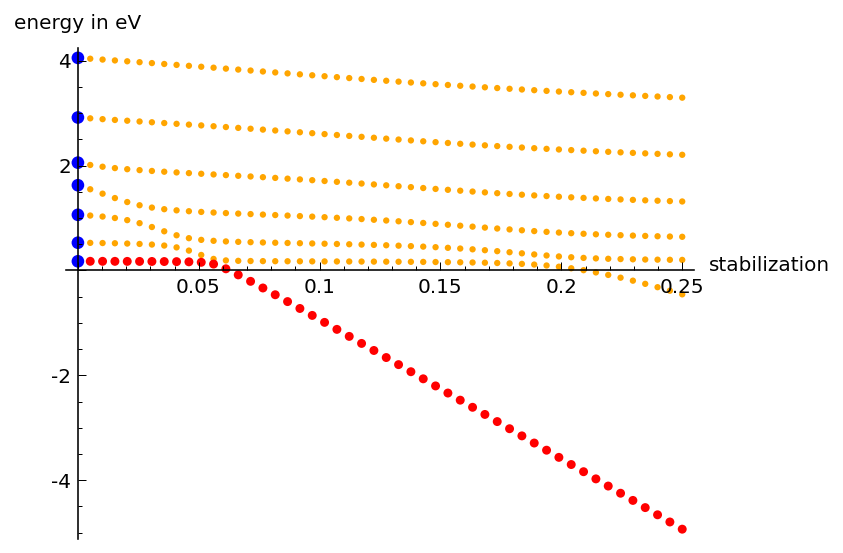
The first project focuses on one special extrapolation method, the analytical continual of the coupling constant (ACCC) method. As in all extrapolation methods, an artificial potential, U, is added to a molecule, however, for the ACCC method to work there is the additional requirement that U is a short-range potential. The potential U helps to stabilize the excess electron at the molecule and can be controlled by a strength parameter, so that the stabilization can be switched on slowly. The data-collection step of the ACCC method then consists of increasing the stabilization until the lowest excess-electron state, which is unbound in the real molecule, is turned into a bound state, and then continuing to increase it until enough bound-state data have been accumulated so that these can be extrapolated back to vanishing stabilization (Scheme 1).

Scheme 1. Data collected in the first step of the ACCC method. The excess-electron states of the molecule (no stabilization) are shown as blue circles, and all of these have a positive energy indicating their instability with respect to electron loss. Once the stabilization is switched on all energies decrease and eventually some of them will become bound states (E < 0). The metastable state itself can be identified by the series of avoided crossings it makes with the discretized continuum states. The second step is then to extrapolate the lowest state (red) back to vanishing stabilization, however, only data to the left of its last avoided crossing is useful for this purpose.

The second step is the back-extrapolation, which is, however, anything but straightforward, because the energy of the metastable states becomes complex when it crosses the threshold (from negative to positive energy): The imaginary part represents the so-called decay width, which indicates that the state is in fact metastable and that it possesses a finite lifetime. A simple linear or quadratic extrapolation of the data will only yield an approximation to the real part, whereas the ACCC method accomplishes the back-extrapolation by extrapolating the energy as a function of a variable that will itself become complex at the point where the bound state crosses into the continuum, so that the energy automatically becomes complex as well.

A more flexible, though computationally more costly method to compute the energy and lifetime of resonances is the complex absorbing potential (CAP) method. Here a CAP is added to the molecular Hamiltonian and its strength is slowly increased so that all eigenvalues become complex. Eigenvalues corresponding to discretized continuum functions quickly gain a large imaginary part, whereas eigenvalues corresponding to resonances stay close to the real axis and show a typical stabilization behavior: They proceed to “their” complex energy, where they slow down until the perturbation by the CAP becomes too strong.

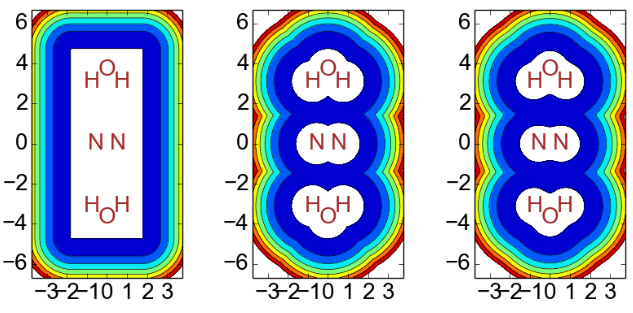
The focus of the current project was the real potential used as a CAP itself (it is then multiplied by i and a constant). In the electronic structure context the potential most frequently used is the so-called box-CAP owing to the ease of its evaluation in a Gaussian basis set (Scheme 2). The box-CAP works well for small, highly symmetrical molecules, but it will clearly be less suitable for larger molecules or molecule clusters, say systems with dangling side-chains. The project tested two new CAP shapes. First, a Voronoi-CAP was examined, where the CAP is defined in each Voronoi cell, the space closes to a given nucleus. This CAP has iso-surfaces, which look like van der Waals surfaces; however, the functions defined this way are continues, but not continues differentiable at the transitions between Voronoi cells possibly giving rise to artificial reflections of the outgoing electron in the CAP calculations. Hence, a second, smooth Voronoi-CAP was also introduced. Cuts through all three potentials are shown below (Scheme 2). A disadvantage of the new potentials is that the integrals have to be evaluated through numerical quadrature, yet with modern computers, that can hardly be called a disadvantage any more.

Scheme 2. Cuts through the three potentials used as boxCAP (left), Voronoi-CAP (middle), the smoothVoronoi-CAP (right) for a N_{2(H2O)2 cluster. The innermost contour is zero, then contours increase by three Hartree.}

Throughout the project it was shown that the new potentials are indeed superior once a molecule or molecule cluster does not fit well into a box and contains “dead space,” that is, space not properly covered by a CAP or by basis functions.

The work I can do because of this grant clearly has a huge impact on my career. Without support for summer research any meaningful professional development at a primary undergraduate institution would be next to impossible. But especially in these times of frugality even activities once taken for granted, such as making presentations at or taking students to regional meetings, become increasingly difficult. Thus, this grant is key to maintaining an active and professional research program as such.

For my students the same is true. It makes a huge difference to know that they do not just participate in some educational project, but in real research that may at some point land them a poster presentation, a trip to a regional or national meeting, or even a co-authorship on a paper. They take their work more seriously, begin to see the value of a deeper level of understanding, and are more likely to continue their research after the mandatory research classes have been taken.