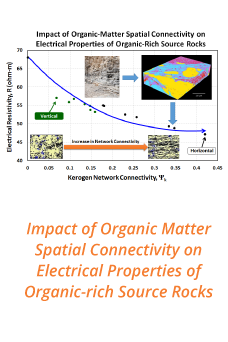
Reports: DNI953783-DNI9: Nonlinear Oscillatory Diffuse Charge Dynamics
Aditya Khair, PhD, Carnegie Mellon University
The objective of this is project is to quantify the nonlinear oscillatory diffuse charge dynamics of electrolytes under large-amplitude, time-dependent voltages. The response of charge-laden media under electric fields plays an important role in the petroleum industry: e.g. application of electrical currents to deep lying reservoirs has been proposed to enhance oil recovery. Electrolytes are also exposed to time-dependent voltages in electrochemical energy storage and conversion devices (e.g. batteries and super-capacitors); ion channels; synthetic nanopores; directed assembly; and microfluidics. The standard technique to characterize transport processes in an electrolyte is Electrochemical Impedance Spectroscopy (EIS), where a sample is subject to a small amplitude ac voltage. The ratio of voltage to measured current equals the complex, frequency-dependent impedance of the material: the real part (in-phase with voltage) yields the resistance, whose inverse is conductivity, and the imaginary part (out-of-phase) yields capacitance. The capacitance is proportional to the electrical energy stored at an electrode-electrolyte interface — a critical quantity for super-capacitors. Equivalent circuit models are frequently used to interpret EIS experiments, wherein the micro-scale ion dynamics are replaced by electronic circuit elements. Crucially, circuit models assume that the impedance is independent of the magnitude of the applied voltage and constant in time, which requires that the current must vary at the same frequency as the imposed voltage. Practically, this scenario is realized only when the maximum amplitude of the applied voltage V0 does not exceed the ‘thermal voltage’ VT = kBT/e, where kB is Boltzmann's constant, T is absolute temperature, and e is the charge on a proton (VT Å 25mV at T = 300K). However, it is common for applied voltages far exceeding VT to be applied across electrolytes, particularly in non-polar solvents relevant to the petroleum industry. In this case, the electrolyte is driven far from equilibrium, and the concept of impedance as a ratio of voltage over current loses meaning. There is a critical gap in understanding of electrolyte dynamics in this nonlinear regime; traditional (linear) EIS has no hope for inferring the conductivity and capacitance at these conditions. This motivates our project to design a modeling framework to extract the physical properties of an electrolyte under large-amplitude, oscillatory voltage.
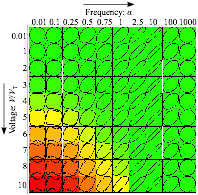
A major accomplishment during the present reporting period was the development of a theoretical model to predict the dynamical response of an electrolyte under a moderately nonlinear oscillatory voltage. This was a central aim of the project proposal. This work was recently published in Physical Review E. Specifically, we quantified the dynamics of a symmetric binary electrolyte between two blocking electrodes under an ac voltage. The diffuse charge dynamics were modeled via the Poisson-Nernst-Planck (PNP) nonlinear partial differential equations for point-like, non-interacting ions. The solution to these equations was expressed as a Fourier series with an asymptotic expansion in voltage for arbitrary Debye layer thickness and ac frequency. The asymptotic expansion proceeded in powers of V0 / VT. We demonstrated that the response of the electrolyte remains essentially linear in voltage amplitude at frequencies greater than the RC frequency of Debye layer charging, D/λDL, where D is the ion diffusivity, λD is the Debye length, and L is half the cell width. In contrast, nonlinear response was predicted at frequencies below the RC frequency (figure 1). The ion densities exhibited symmetric deviations from the (uniform) equilibrium density at even orders of the voltage amplitude. This led to the voltage dependence of the current in the external circuit arising from the odd orders of voltage expansion. The first nonlinear contribution to the current is O(V03) and contains a third harmonic overtone and a component oscillating at the applied (fundamental) frequency. These results were used to compute a generalized voltage-dependent impedance, the first nonlinear contribution to which is quadratic in V0. This contribution predicts a decrease in the imaginary part of the impedance at low frequency, which is due to the increase in Debye layer capacitance with increasing V0. In contrast, the real part of the impedance increases at low frequency, due to adsorption of neutral salt from the bulk to the Debye layer. In summary, we demonstrated that a meaningful notion of impedance could be formulated beyond the small-voltage regime, which encodes physical information on electrolyte response under larger voltages. Moving forward, we are developing a numerical spectral element scheme to solve the PNP equations under strongly nonlinear ac voltages, far exceeding VT, which is a natural next step. Moreover, we aim to validate our theoretical predictions against experimental measurements, which will be performed in collaboration with Profs. D. Prieve and P. Sides at Carnegie Mellon University.
Figure 1: Computational map for diffuse charge dynamics under ac voltage between blocking, parallel electrodes. Each panel displays a Lissajous curve of current versus voltage at a dimensionless ac frequency a and voltage V0 /VT . (Frequency is normalized by RC time for double-layer charging.) The color scheme is from green (linear response) to red (nonlinear response). In linear EIS (small voltages) all Lissajous curves are elliptical. Even at large voltages the response is linear at large frequency. Nonlinear impedance, corresponding physically to nonlinear Debye layer capacitance and neutral salt adsorption, can be extracted from the deformed (non-elliptical) shapes at large voltage and low frequency (bottom left corner).
The scientific impact of this research includes one journal publication and an oral presentation at the ACS Colloid and Surface Science Symposium in June 2015. The research has provided partial support for two graduate students, Robert Stout and Nicholas Chisholm, who have received advanced training in electrochemical dynamics and applied mathematics. Stout is a fourth year student who spearheaded the published work on electrolyte dynamics under a moderate voltage and gave the oral presentation at the ACS symposium. Chisholm is a fourth year student who is developing the numerical spectral element scheme mentioned above. The project funding has positively impacted the Principal Investigator's career by facilitating continuation of his research interests in electrochemical transport processes.