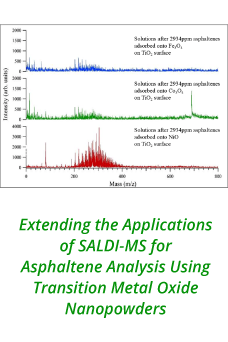
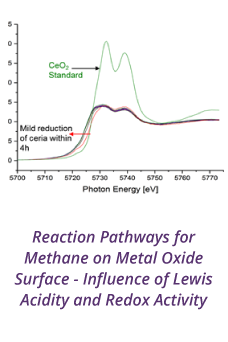
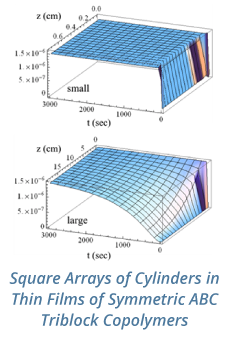
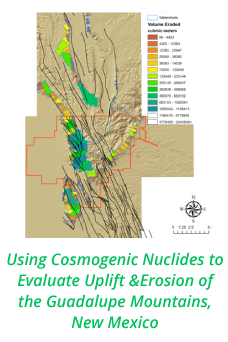
Reports: DNI953924-DNI9: A Fundamental Investigation of Turbulence in Multiphase Gas-Particle Flows
Alberto Passalacqua, PhD, Iowa State University
The proposed research aims at studying the fundamental mechanisms of turbulent interaction between the fluid and the dispersed phase in multiphase dispersed flows by using mesoscale direct numerical simulations (DNS). Such simulations are performed by solving continuum equations to describe both phases, with spatial and temporal resolution sufficient to ensure that all the turbulent scales are directly described by the methodology.
Results obtained from the mesoscale DNS will allow to quantify important terms that appear in models for turbulent gas-particle flows (diffusion of turbulent kinetic energy (TKE), TKE flux internal to each phase, production and dissipation of TKE, flux of granular energy) and, more importantly, coupling terms like velocity-volume fraction, volume fraction-pressure, and fluid-particle velocity covariances. Constitutive relations for these terms, suitable to be used in multiphase Reynolds-average (RA) turbulence models, will be provided and tested, in order to improve their predictive capabilities.
While this research was focused on riser flows in the original proposal, it appears to be more appropriate to consider the general framework of multiphase disperse flows as reference, rather than limiting the attention to riser flows at this stage. This allows a more general formulation of the Reynolds-averaged multiphase flow equations, since forces such as lift and virtual mass will be also considered. These forces are usually neglected in the simulation of riser flows, but play a significant role in gas-liquid systems (bubble columns, air-lift reactors, stirred tank reactors), which are particularly relevant to the petroleum industry. Based on this consideration, meso-scale direct numerical simulations were performed in the computational domain illustrated in Fig. 1. The density of the fluid was considered to be 1000 times higher than the density of the dispersed phase, which was considered to be monodisperse and spherical. This is equivalent to consider buoyant spherical particles in a fluid to mimic a gas-liquid flow.
Fig. 1: Schematic representation of the computational domain.
Periodic boundary conditions were applied on all the sides of the column, allowing the RA equations for momentum and turbulent properties to be simplified by eliminating the terms containing the gradient of the statistics. In order to prevent the liquid from accelerating, a body force was added to the liquid momentum equation.
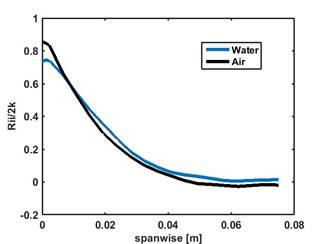
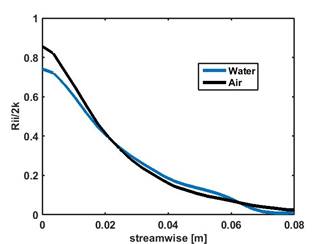
The influence of the periodic boundary condition on the statistics is eliminated by choosing a domain size based on the velocity pair correlation function [6] as shown in Fig. 2 and 3. The plots indicates that pair correlation function approaches zero before the end of the domain both in span-wise and stream-wise direction, which indicates the computational domain is suitable to perform the simulations.
Fig. 2: Spanwise pair correlation function.
Fig. 3: Streamwise pair correlation function.
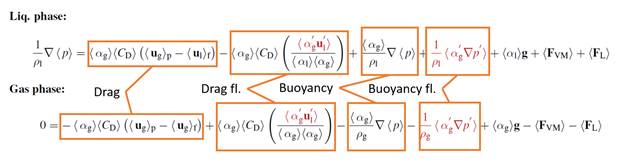
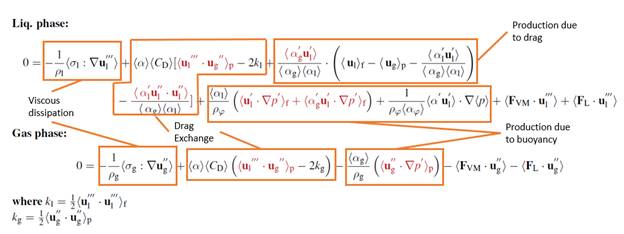
Volume fractions of dispersed phase between 10 and 50% were considered, with a mean-slip particle Reynolds number of 1600. The investigation was started with the highest volume fraction of disperse phase (50%), which was completed, while cases with volume fraction of 10% and 30% are in progress. A budget of the terms in the RA momentum equation was computed, and is summarized in Tab. 1, where quantities were normalized with respect to the mean drag force, and “fl.” Indicates the unclosed term due to fluctuations in the corresponding force term, as highlighted in Eq. 1.
Eq. 1: Reynolds-averaged phase momentum equation in the periodic box.
|
Phase |
Drag |
Buoyancy |
Drag fl. |
Buoyancy fl. |
Gravity |
Added force |
Lift fl. |
Virtual mass fl. |
|
Liquid |
1 |
-1.2130 |
-0.2849 |
0.0778 |
-2.2860 |
2.4260 |
0.0278 |
0.0567 |
|
Gas |
-1 |
1.2130 |
0.2849 |
-0.0778 |
-0.0028 |
- |
-0.0278 |
-0.0567 |
Tab. 1: Momentum budget with 50% volume fraction of the disperse phase.
The contribution of the unclosed term resulting due to the RA of the drag force resulted to be one order of magnitude higher than the unclosed terms due the RA of lift, virtual and buoyancy force. This indicates that the accurate description of this term by computational models is key in accurately describing these flows.
|
Phase |
Drag exchange (J/m3s) |
Production due to drag |
Production due to buoyancy |
Lift |
Virtual mass |
Viscous dissipation |
|
Liquid |
145.9192 |
181.1664 |
-210.24 |
65.08 |
-188.85 |
-2.34 |
|
Gas |
-312.3904 |
- |
58.64 |
-43.88 |
151 |
-0.1540 |
Tab. 2: Turbulent kinetic energy budget with 50% volume fraction of the dispersed phase.
Data in Tab. 2 indicate that the contribution of all the inter-phase forces are important for what concerns the budget of the turbulent kinetic energy equation (Eq. 2).
Eq. 2: Turbulent kinetic energy equation in the periodic box.
In the gas phase, the contribution of drag is higher compared to other forces. However, in the liquid phase the contribution of the buoyancy force is higher than all the other forces. Additionally, the contribution of the virtual mass towards liquid TKE is negative indicating that it appears to be dissipative in nature.
The analysis of the components of the Reynolds stresses for the phases shows a significant anisotropy in the direction of the gravitational acceleration. For example, the components of the Reynolds stress for the gas phase found from meso-scale DNS are Rxx = Ryy = 0.096 Pa and Rzz = 0.288 Pa. For the liquid phase the normal components of the turbulent stress tensor are Rxx = Ryy = 40 Pa, and Rzz = 153 Pa. Fluctuations in the direction of the gravitational acceleration are therefore predominant, and show that models which rely on the isotropy assumption of turbulent fluctuations may fail, since the hypothesis they rely on is not respected by the system they are applied to.
In the remainder of the project, the meso-scale DNS will be completed, the RA terms appearing in the momentum and turbulence Reynolds stress equations will be quantified and closed based on the numerical results obtained from the meso-scale DNS.