60th Annual Report on Research 2015

Materials

The polymer solution studied in this work is polystyrene (PS)/diethyl phthalate (DEP) solution. The linear PS was purchased from Polymer Source. The M_n is 980,000 g/mol and PDI is 1.16. High purity (99.5%) DEP was purchased from Sigma-Aldrich. 10% PS/DEP solutions were prepared by following the method provided in the work of Qin et al. (2009) [1]. The concentration of the solution was calculated by the mass of the PS and DEP added into the system before evaporation of the co-solvent.

Methods

Strain Controlled Mechanical Spectral Hole Burning (MSHB) experiments were performed with a TA Instruments ARES rheometer with a 25 mm diameter and 0.1 rad angle cone and plate fixture. The truncation gap was 0.056 mm. A 2KFRTN1 force rebalance transducer with a torque range of 2000 g cm was used. The MSHB experiments were performed at -40 ºC.

Stress Controlled MSHB experiments were carried out on an MCR 501 (Anton Paar GmbH) with a 25 mm diameter cone and plate fixture. The cone angle is 6°, and the truncation gap is 0.047 mm. Dynamic amplitude sweep tests were performed to determine the linear stress region at -40 ºC. The MSHB tests were performed at the same temperature.

Results and Discussion

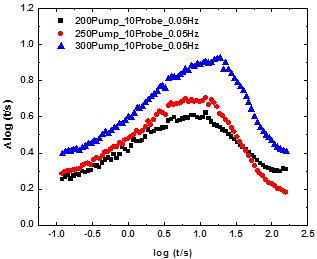
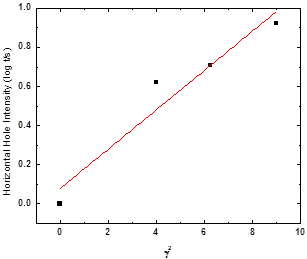
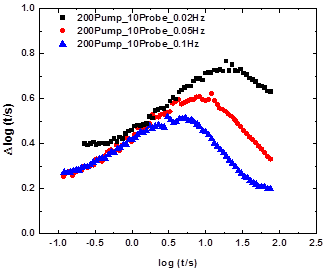
The Strain controlled MSHB experiments were performed at 0.05 Hz. The probe strain was 10%. Since previous work has shown that no complete vertical holes form in the test window, here we only show the results for horizontal holes. Fig. 1 shows the complete horizontal holes at different pump strain amplitudes, which demonstrates the dynamic heterogeneity in the system. The hole intensity increases as the pump amplitude increases and shifts to longer times. In Fig. 2 we show a plot of the hole intensity vs. the square of pump amplitude. A quadratic dependence is observed. A similar dependence has been reported in previous MSHB work [2] and in the dielectric analogue[3, 4]. In Fig. 3 we show horizontal holes obtained at different frequencies. As the frequency decreases, the hole intensity increases and shifts to longer times, consistent with prior findings[1].

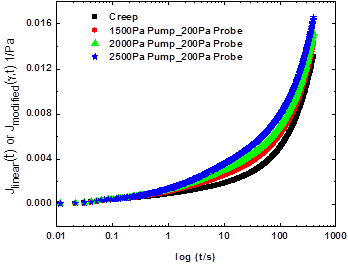
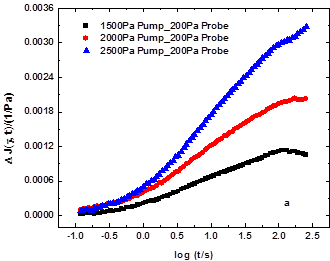
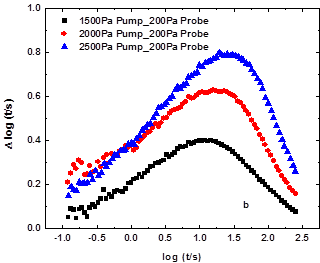
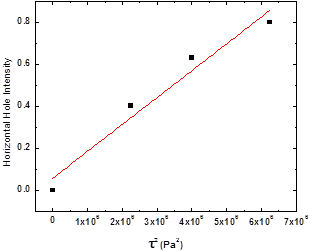
LAOS experiments are generally performed in strain control, i.e., where a sinusoidal strain pump is applied and the resulting nonlinear stress output is measured. Recently, several works[5-9] have expanded LAOS into the stress controlled condition, which is more analgous to the dielectric compliances used in dielectric hole burning tests. Therefore, we have extended the study to the stress controlled regime to compare the results with the strain controlled MSHB. Fig. 4 shows the linear and modified creep compliances at different pump stresses for a probe stress of 200 Pa. Accordingly, the mechanical holes are calculated and shown in Fig. 5. Similar to the strain controlled MSHB, incomplete vertical holes are observed in Fig. 5(a). However, it seems that for the 1500 Pa pump stress, vertical holes may be forming at long times. As seen in Fig. 5(b), complete horizontal holes are formed for all three cases, consistent with heterogeneous dynamics in the system. As shown in Fig. 6, the hole intensity increases linearly with the square of pump stress amplitude.

Figure 1. Horizontal holes of Strain Controlled MSHB results for 10% PS/DEP at -40 ºC at 0.05 Hz with 10% probe strain at different pump strain.

Figure 2. Horizontal hole intensity vs. square of the pump strain amplitude.

Figure 3. Horizontal holes of Strain Controlled MSHB results for 10% PS/DEP at -40 ºC with 200% pump strain and 10% probe strain at different frequencies.

Figure 4. Linear and modified time dependent creep compliances for 10% PS/DEP solution

Figure 5. MSHB results for 10% PS/DEP at -40 ºC at 0.05 Hz with 200 Pa probe stress: (a) Vertical intensity vs. log t and (b) horizontal response vs. log t, both for different pump stresses.

Figure 6. Horizontal hole intensity vs. the pump stress amplitude.

Conclusions

Strain controlled and stress controlled MSHB experiments were performed to study the nonlinear response of 10% PS/DEP solutions in the rubbery plateau regime. In both cases, complete horizontal holes are observed, and the hole intensity increases quadratically with increasing pump strain or stress amplitude increases. While incomplete vertical holes are found for all tested conditions for the strain controlled MSHB tests, for the stress controlled MSHB tests, complete vertical holes appear at long times.

Future Work

Further experiments will focus on comparison of strain controlled and stress controlled MSHB experiments. And combine the Fourier Transform Rheology and Lissajous-Bowditch loops to build more complete fingerprinting techniques to investigate the nonlinear response. Chain architecture effects will also be studied.

References

1. Qin, Q.; Doen, H.; McKenna, G. B. Mechanical Spectral Hole Burning in Polymer Solutions, J Polym Sci Pol Phys 2009, 47, (20), 2047-2062.

2. Shamim, N.; McKenna, G. B. Mechanical spectral hole burning in polymer solutions: Comparison with large amplitude oscillatory shear fingerprinting, J Rheol 2014, 58, (1), 43-62.

3. Schiener, B.; Bohmer, R.; Loidl, A.; Chamberlin, R. V. Nonresonant spectral hole burning in the slow dielectric response of supercooled liquids, Science 1996, 274, (5288), 752-754.

4. Schiener, B.; Chamberlin, R. V.; Diezemann, G.; Bohmer, R. Nonresonant dielectric hole burning spectroscopy of supercooled liquids, J Chem Phys 1997, 107, (19), 7746-7761.

5. Lauger, J.; Stettin, H. Differences between stress and strain control in the non-linear behavior of complex fluids, Rheol Acta 2010, 49, (9), 909-930.

6. Bae, J. E.; Lee, M.; Cho, K. S.; Seo, K. H.; Kang, D. G. Comparison of stress-controlled and strain-controlled rheometers for large amplitude oscillatory shear, Rheol Acta 2013, 52, (10-12), 841-857.

7. Dimitriou, C. J.; Ewoldt, R. H.; McKinley, G. H. Describing and prescribing the constitutive response of yield stress fluids using large amplitude oscillatory shear stress (LAOStress), J Rheol 2013, 57, (1), 27-70.

8. Ewoldt, R. H. Defining nonlinear rheological material functions for oscillatory shear, J Rheol 2013, 57, (1), 177-195.

9. Mendes, P. R. D.; Thompson, R. L.; Alicke, A. A.; Leite, R. T. The quasilinear large-amplitude viscoelastic regime and its significance in the rheological characterization of soft matter, J Rheol 2014, 58, (2), 537-561.