60th Annual Report on Research 2015

The aim of this work is the formulation of methods for calculation of free energies of crystalline solids, and their application to calculation of the phase diagram of model clathrate hydrates, considering a variety of guest molecules. In pursuing this goal, we have (1) discovered a very powerful, general method for computing properties of crystals by molecular simulation, and we have demonstrated this method with several model systems. The method takes harmonic behavior as a starting point, and provides full (anharmonic) properties very efficiently by molecular simulation; (2) we have performed very careful calculations of harmonic properties of a clathrate structure of water, with particular attention to finite-size effects; (3) we have realized that the method described for crystals in (1) is in fact a special case of a much more general method to synthesize approximate models with molecular simulation. This development has potential for great impact to molecular modeling methods, and it is currently under active development. Details follow.

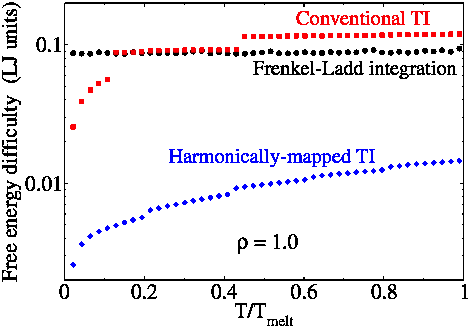
(1) Harmonically mapped averaging. We have introduced knowledge of approximate harmonic behavior of crystals is into a new “mapped averaging” framework (see (3)) to yield alternative expressions for the thermodynamic properties of crystalline systems. The expressions separate the known harmonic behavior from residual averages, which thus encapsulate anharmonic contributions to the properties. With harmonic contributions removed, direct measurement of these anharmonic contributions by molecular simulation can be accomplished without contamination by noise produced by the already-known harmonic behavior. We show with application to the Lennard-Jones model that first-derivative properties (pressure, energy) can be obtained to a given precision via this harmonically-mapped averaging at least 10 times faster than by using conventional averaging, and second-derivative properties (e.g., heat capacity) are obtained at least 100 times faster --- in more favorable cases, the speedup exceeds a millionfold. As shown in the first figure, free-energy calculations are accelerated by 50 to 1000 times. The plot presents the difficulty, a measure of the uncertainty obtained for a given amount of computational effort. The CPU-time requirement for a calculation of a given precision then goes as the square of this quantity. The figure shows the new approach (Harmonically-mapped thermodynamic integration) against conventional thermodynamic integration, and the widely-used Frenkel-Ladd method. Calculations are for the Lennard-Jones model.

Data obtained using the mapped-average formulations are rigorous and not subject to any added approximation, and in fact are less sensitive to inaccuracies relating to finite-size effects, potential truncation, equilibration, and similar considerations. Moreover, the approach does not require any alteration in how sampling is performed during the simulation, so it may be used with standard Monte Carlo or molecular dynamics methods. However, the mapped averages do require evaluation of first and second derivatives of the intermolecular potential, for evaluation of first and second thermodynamic-derivative properties, respectively. Apart from its usefulness to simulation, the formalism developed by us may constitute a basis for new theoretical treatments of crystals.

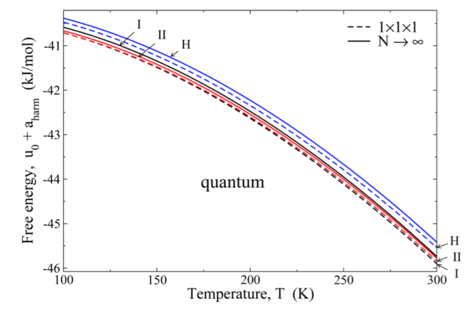
(2) Lattice-dynamics of hydrates. The mapped-averaging method requires knowledge of harmonic behavior as an input, so to enable the targeted application to clathrate hydrates, we considered lattice dynamics methods for calculation of the free energy of clathrate hydrate phases, specifically the cubic structure I (sI), cubic structure II (sII) and hexagonal structure H (sH) phases, in the absence of guest molecules. We examined in particular the effects of finite size and proton disorder on the calculated free energies, and considered these in the context of the free-energy differences between the phases. We find that at 300 K, the finite-size, proton-disorder, and quantum effects between phases are, respectively, on the order of 0.4 kJ/mol, 0.03 kJ/mol, and 0.1 kJ/mol. We published a very detailed description of the calculations, which can be quite tedious to implement, with emphasis on efficiencies developed to handle various aspects related to multiatomic lattice dynamics with electrostatic interactions in large crystalline systems. The following figure shows an example of the results we obtained. This presents the quantum harmonic Helmholtz free energy per molecule for the sI, sII, and sH structures as a function of temperature, both in the thermodynamic limit (solid lines) and for a single unit cell (dashed lines). The figure shows that finite-size effects (among other considerations) are large enough to affect the ordering of the stability of the phases, so it is important to account for them properly.

(3) General mapped averaging. We have found that the harmonically-mapped averaging method is one example of a general mapped-averaging method that can be used to leverage approximate treatments to produce simulation methods with much higher efficiency than currently possible. We have just begun to explore the possibilities, but we have found for example that the dielectric constant can be computed much more efficiently in this manner, and we are currently developing a method for calculation of the pressure of fluid phases. We have also formulated a means to measure temperature in NVE simulations that exploits the same idea underlying harmonically mapped averaging. We are in the end stages of developing these ideas and generating results, and we expect that publications and presentations based on this work will be submitted in the coming months.