60th Annual Report on Research 2015

Summary: The goal of the research project was to study the formation of methane clathrate hydrate using MD simulation coupled with recently developed analysis tools. These "small-N" cluster analysis tools yield cluster free energies from equilibrium cluster size distributions, even in cases where relatively few clusters are present and the law of mass action does not apply.  Taking the advice of the proposal's reviewers, we have pursued some less complex systems in order to refine our methods before tackling the original problem. 

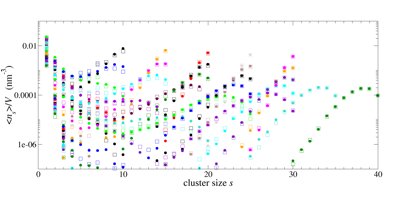
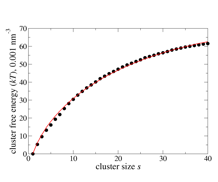
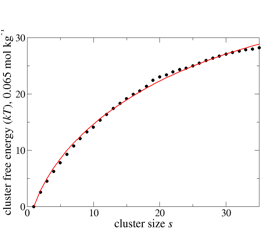
Nucleation of liquid MTBE from vapor and solution phases:  Methyl t-butyl ether (MTBE) is a fuel additive whose moderate solubility in water has led to issues with environmental contamination, and also places it in a convenient range for computational study of the formation of MTBE clusters in water.  To explore the capabilities and limitations of the small-N methods, MTBE cluster formation in vapor and solution environments have been studied.  A total of 28 systems containing between 10 and 40 MTBE molecules in the gas phase were simulated for 1 µs at 273 K at 4 densities above and below the expected vapor pressure, using the TraPPE force-field.¹  Data from all simulations (Figure 1) could be fit with a single set of cluster free energies (Figure 2, filled circles) using a new global fitting procedure based on previous² methods. The size dependence of the free energies in turn agreed with the form expected from classical nucleation theory (CNT) (Figure 2, red curve) for clusters containing more than 10 monomers.

Figure 1: Simulation data (filled circles) and "small-N" analysis fits (open squares) for all gas-phase MTBE data sets simulated.

Figure 2:  Optimized values for MTBE vapor-phase cluster free energies used to obtain fits in Figure 1 (circles), with CNT fit (red curve.)

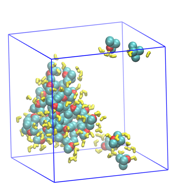
MTBE in water was next used as a test of the use of "small-N" methods for studying cluster growth from aqueous solution. Between 10 and 35 MTBE molecules were simulated in a cubic water box containing about 2000 TIP4P³ water molecules; a snapshot showing a cluster and unassociated MTBE is shown in Figure 3.

Figure 3.  35 MTBE (cyan and red) with TIP4P water (yellow) at 273 K, only showing waters within 3.5 .

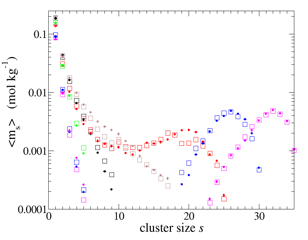
Association constants were calculated using the small-N analysis method just as for vapor-phase MTBE (Figures 4 and 5).  Again, CNT was effective in fitting to the cluster free energies over the full range measured (see red curve in Fig. 5).  Our next step will be to calculate the surface tension at the liquid water/ MTBE interface in an independent simulation to compare with the value obtained from the CNT fit.

Figure 4.  Cluster size distributions – as average molalities - obtained from simulations with 10-35 MTBE and ~2000 water over 500 ns at 273 K. Solid circles are simulation data, open squares are fits to the cluster free energy function.

Figure 5.  Cluster free energy function for aqueous MTBE.  Solid circles are individual cluster free energies used to optimize fit in Fig. 4.  Red curve is best two-parameter fit to CNT expression.

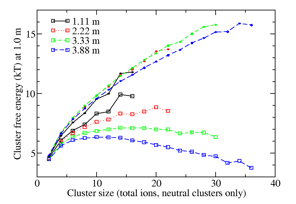
Formation of amorphous NaCl clusters from aqueous solution: Evidence from recent simulation studies by Chakraborty and Patey⁴ suggests that the formation of a dense amorphous NaCl phase precedes formation of ordered crystallites.  Here we investigate the formation of the amorphous clusters themselves.  In an initial test application to small clusters of Na⁺ and Cl^- at moderate concentration, using the same parameters as ref. ⁴, we found strong concentration dependences in the best-fit cluster free energies (Fig. 4, open squares) which implies that the equilibrium constants are not constant.  Hypothesizing that this breakdown arose from the crowding among ions and clusters (with their solvent shells), we adapted the small-N analysis method to account for the excluded volume effects of clusters' solvent shells.  We analyzed the solvation structure observed during simulations and determined the mean number of solvents associated with s-mer clusters.  The small-N cluster analysis was repeated with the effective volume of the system reduced by half of the total volumes of the clusters' solvent shells; the factor of one-half reflects the ability of the same water to solvate two ions.  In dilute systems, this had a negligible effect on the relative probabilities of large and small clusters, but at high concentration it produced a shift towards large clusters, as water to solvate fully separated ions becomes scarce.   Agreement between the recalculated cluster free energy curves at different concentrations in Figure 4 (filled circles) indicates success in disentangling intrinsic cluster stability from crowding effects.

Fig. 6.  Cluster free energies of neutral NaCl clusters from fitting of full binary cluster distributions for 20 NaCl solvated with water simulated over 500 ns at 300 K.  Open squares are based on ideal cluster mixing with solvent; filled circles are corrected for crowding effects.

Career impact on supported personnel: A Ph.D. student supported by this project, Lara Bolling-Patel, has made important strides towards understanding the thermodynamics of association in vapor-phase and aqueous methyl t-butyl ether (MTBE) and in aqueous sodium chloride.  In addition to supporting her stipend and paying for essential computational resources, this funding allowed her (and the P.I.) to attend the American Physical Society March Meeting and present research talks; she is currently preparing a manuscript for publication.  The results obtained have been included in a recently submitted NSF proposal by the P.I.

(1)      Stubbs, J. M.; Potoff, J. J.; Siepmann, J. I. Transferable Potentials for Phase Equilibria. 6. United-Atom Description for Ethers, Glycols, Ketones, and Aldehydes. J. Phys. Chem. B 2004, 108, 17596-17605.

(2)      Kindt, J. T. Accounting for Finite-Number Effects on Cluster Size Distributions in Simulations of Equilibrium Aggregation. J. Chem. Theory Comput. 2013, 9, 147-152.

(3)      Jorgensen, W. L.; Chandrasekhar, J.; Madura, J. D.; Impey, R. W.; Klein, M. L. Comparison of Simple Potential Functions for Simulating Liquid Water. J. Chem. Phys. 1983, 79, 926-935.

(4)      Chakraborty, D.; Patey, G. N. Evidence That Crystal Nucleation in Aqueous Nacl Solution Occurs by the Two-Step Mechanism. Chem. Phys. Lett. 2013, 587, 25-29.