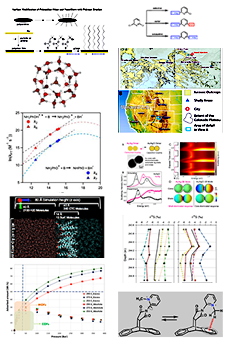
Reports: ND954593-ND9: Confinement Effect on Solubility of Oilfield Fluids in Sub-Micron Pores
Keith E. Gubbins, PhD, North Carolina State University
We have carried out a study of the influence of confinement in slit-shaped carbon pores on the solubility of a supercritical gas in a liquid solvent, by combining Gibbs Ensemble Monte Carlo (GEMC) simulation and classical density functional theory (DFT). The model mixture chosen for our primary study was a simple model of methane as the solute gas in liquid benzene as the liquid solvent. We considered both graphite and silica slit-shaped pores, and obtained results for the influence of pore width, temperature and bulk phase pressure on the solubility and the adsorption. We further considered a model mixture of hydrogen and octamethylcyclotetrasiloxane (OMCTS) in silica and graphite slit pores, a system for which the solute gas, H2, interacts very weakly with both the solvent and the pore walls.
Previous reports of solubility in confinement have used a variety of different definitions of such solubility, with many reporting the overall density of solute in the pore, ![]() , in mmol.cm-3 as the solubility of the solute, 2. With such a definition most systems will exhibit excess adsorption due to the strong adsorption forces, and this has been termed "over-solubility". Such a definition of "solubility" suffers from two drawbacks in practice. It does not take into account the increase in density of the solvent in the pore, which is often substantial, so that the state of the confined solvent is not truly comparable to that of the bulk mixture. Secondly, this measure of solubility rests on a somewhat arbitrary operational definition of the accessible pore volume. We have proposed the mole fraction of solute in the pore,
, in mmol.cm-3 as the solubility of the solute, 2. With such a definition most systems will exhibit excess adsorption due to the strong adsorption forces, and this has been termed "over-solubility". Such a definition of "solubility" suffers from two drawbacks in practice. It does not take into account the increase in density of the solvent in the pore, which is often substantial, so that the state of the confined solvent is not truly comparable to that of the bulk mixture. Secondly, this measure of solubility rests on a somewhat arbitrary operational definition of the accessible pore volume. We have proposed the mole fraction of solute in the pore, ![]() , as a more meaningful measure of the solubility, S2, since it takes into account increased solvent density and avoids having to define the accessible volume. With this latter definition we observed both over- and under-solubility, depending on the values of the variables (potential parameters, state conditions) that characterize the system. The two measures of "solubility",
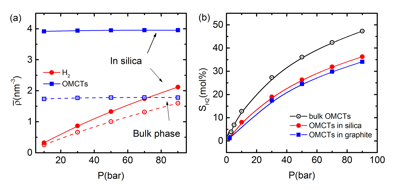
, as a more meaningful measure of the solubility, S2, since it takes into account increased solvent density and avoids having to define the accessible volume. With this latter definition we observed both over- and under-solubility, depending on the values of the variables (potential parameters, state conditions) that characterize the system. The two measures of "solubility", ![]() and S2, lead to substantially different results and conclusions concerning confinement effects on solubility, as seen in Figure 1. Thus, for the H2/OMCTS mixture in silica pores (Fig. 1) we observe "over-solubility" when
and S2, lead to substantially different results and conclusions concerning confinement effects on solubility, as seen in Figure 1. Thus, for the H2/OMCTS mixture in silica pores (Fig. 1) we observe "over-solubility" when ![]() is used, but observe "under-solubility" when the more appropriate S2 is plotted.
is used, but observe "under-solubility" when the more appropriate S2 is plotted.
Figure 1. (a) Effect of bulk pressure on the density of hydrogen and OMCTS in the bulk phase and in silica slit pores of width H=3.4nm, at a temperature T=323 K, from DFT. Hollow symbols are values in the bulk phase while solid lines are values in the pore. (b) Solubility of hydrogen in OMCTS for the bulk solvent and confined in silica and graphite slit pores of width H=3.4nm, at a temperature T=323 K, from DFT. Lines are a guide for the eye.
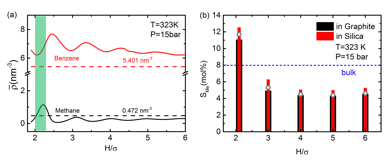
We find that when confined within graphite or silica slit pores the solubility of methane, S2, in benzene is strongly dependent on the pore width, and under-solubility is usually observed when the pore width is large (Figure 2). However, for certain narrow ranges of pore width, where the solvent molecules are less tightly packed, over-solubility is observed. We argue that this phenomenon results from the competition of two mechanisms. The first one is a packing effect; for pore sizes where the adsorbed layers of solvent benzene are less tightly packed, more methane molecules can be accommodated in the pore. When the pore width is large, a competitive adsorption mechanism dominates, and the solubility depends on the relative strengths of the adsorbate-wall and solvent-solute interactions.
Figure 2. Methane uptake at 323 K and 15 bar bulk pressure in slit pores of various pore widths. (a) adsorption (number of molecules/nm3) of methane and benzene in different graphene slit pores from DFT with reduced pore width ![]() ranging from 1.9 to 6.0; (b) methane solubility in representative pores with pore widths
ranging from 1.9 to 6.0; (b) methane solubility in representative pores with pore widths ![]() =2.1, 3.0, 4.0, 5.0 and 6.0. Bars are results from DFT in graphite (black) and silica (red); gray circles are results from GEMC in graphite under the same condition.
=2.1, 3.0, 4.0, 5.0 and 6.0. Bars are results from DFT in graphite (black) and silica (red); gray circles are results from GEMC in graphite under the same condition.
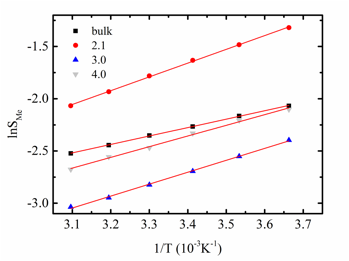
Increase in the temperature results in a decrease in the gas solubility, as for the bulk phase. If the solubility is small, the rate of change of the solubility with temperature increase is proportional to the enthalpy change on solution in the pore, ![]() . This can be determined from the slope of the plot of
. This can be determined from the slope of the plot of ![]() vs.
vs. ![]() (Figure 3). For the bulk liquid phase, this enthalpy change for our model system is -6.96 kJ/mol. For the confined mixture it is larger in magnitude, due to the strong interactions with the carbon walls, and increases as the pore width decreases. For pores of width 2.1
(Figure 3). For the bulk liquid phase, this enthalpy change for our model system is -6.96 kJ/mol. For the confined mixture it is larger in magnitude, due to the strong interactions with the carbon walls, and increases as the pore width decreases. For pores of width 2.1 ![]() it is -10.96 kJ/mol. Thus for the confined mixture the solubility decreases more rapidly with increasing temperature than for the bulk mixture.
it is -10.96 kJ/mol. Thus for the confined mixture the solubility decreases more rapidly with increasing temperature than for the bulk mixture.
Figure 3. The effect of temperature on the solubility of methane in benzene, for both the bulk solvent and for the solvent in slit pores of various pore widths, at 15 bar bulk pressure.
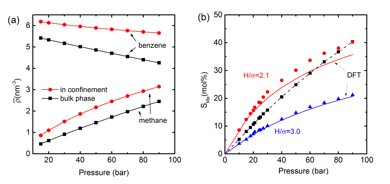
Increase in the bulk phase pressure causes the solubility in the pore to increase, as for the bulk liquid mixture, and Henry's law is obeyed for sufficiently low pressures (Figure 4). The requirement for Henry's Law to hold is that the solution is sufficiently dilute that solute-solute interactions are negligible. This requirement is less easily satisfied in the pores, since the solute molecules are no longer uniformly distributed in the pore.
Figure 4. (a) Effect of bulk pressure on the overall density of methane and benzene in bulk and in a graphite slit pore of H=2.1 ![]() at temperature T=323 K. All data points are from DFT. Lines are a guide for the eye. (b) Solubility of methane in benzene at 323 K. Symbols are GEMC simulation results while the solid lines present the DFT prediction. The black squares are the bulk solubility; the dash line is a guide for the eye.
at temperature T=323 K. All data points are from DFT. Lines are a guide for the eye. (b) Solubility of methane in benzene at 323 K. Symbols are GEMC simulation results while the solid lines present the DFT prediction. The black squares are the bulk solubility; the dash line is a guide for the eye.