61st Annual Report on Research 2016

This summary of our research during the past year reports on two primary research activities.

Correlation for Sessile Drop Evaporation

To better understand how the evaporation of sessile drops and small puddles is controlled by the vapor phase transport mechanisms of mass diffusion and buoyancy-induced (natural) convection, the evaporation rates of eight hydrocarbon liquids evaporating under a broad range of ambient conditions were correlated with physical and geometrical properties. The correlation provides a simple equation involving conventional parameters for diffusive and convective transport. Examination of the correlation equation provides valuable insight into how the roles of diffusive and convective transport change with physical and geometrical parameters; and the correlation is much easier to implement than a computational model based on the coupled conservation equations of mass, energy, and momentum for the two phases. In addition, the correlation provides a simple method for predicting evaporation rates and thus can be a valuable tool to help validate complex computational models and to aid in the analyses of applications involving sessile drop evaporation.

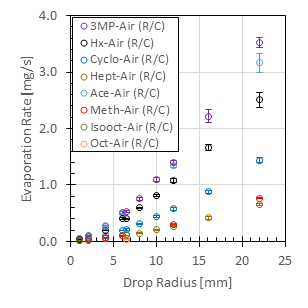
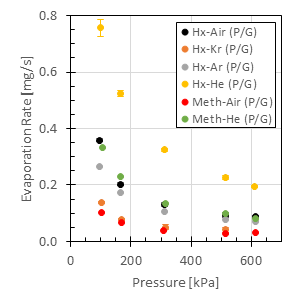
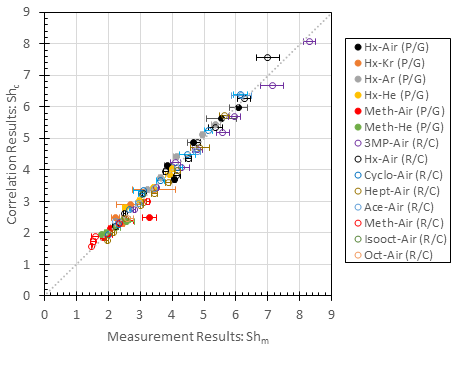
The correlation fits measurements of two series of experiments which were designed to control the relative effects of vapor phase diffusion and buoyancy-induced convection. In all of the experiments, the drop/puddle was contained on a flat aluminum substrate and the drop was “pinned” so that the contact area between the drop and the solid surface remained constant during the measurements. In one series of experiments, the rates of evaporation into air of eight hydrocarbons were measured for a broad range of drop radii from 1mm to 22mm. (The large drops are more aptly described as puddles.) This set of experiments was conducted at atmospheric pressure. A second series of experiments was conducted for which the drop was placed in a pressure-vessel, which enabled the pressure and the ambient gas surrounding the drop to be controlled. The evaporation rates of two hydrocarbons, hexane and methanol, evaporating into four different gases at pressures from 1 to 6 atmospheres were measured. The gases were selected to provide a broad range of mass diffusivities and a broad range of differences between the vapor and gas densities. The ratio of that density difference to the ambient gas density (the density difference ratio) is the driving potential for buoyancy-induced convection. Taken together, the two series of experiments covered a factor of 16.7 variation in liquid volatility as indicated by the equilibrium vapor pressures, a factor of 52.2 variation in mass diffusivities, a factor of 3,557 variation in the density difference ratios, and a factor of 22 variation in drop radii. As a result, the correlation is applicable to a very broad range of conditions. All of the experiments were conducted at room temperature, 22.6°C, in order to avoid currents in the ambient gas due to thermally-induced natural convection. The evaporation rate measurements are shown in Fig. 1 and the results of the correlation, which is expressed in terms of the dimensionless Sherwood number are shown in Fig. 2. The correlation predicts the measurements to within an rms error of 6%.

Fig. 1a.  Measured evaporation rates in air at 1 atm and 23°C as a function of drop size.

Figure 1b.  Measured evaporation rates in a variety of background gases as a function of ambient pressure.

Figure 2.  Comparison of the Sherwood number computed by the correlation, Sh_c, to the Sherwood number determined by the evaporation rate measurements, Sh_m, for all of the data. If the correlation were perfect, all of the data would lie on a line passing through the origin with a slope of 1.

Uncertainty Analysis of Vapor Distribution Measurements

In previous years, we had developed a technique to measure the vapor distribution surrounding an evaporating sessile drop. We are now working on computing the diffusive flux at all locations within the measured vapor distributions and, through comparison with our evaporation rate measurements, to infer the rate of natural convection. The ability to obtain meaningful computational results for the diffusive flux depends on the magnitude of the uncertainty of our experimental results, which is difficult to assess because the experimental technique involves complicated mathematical procedures. In order to compute and evaluate the uncertainty in the experimental results, a computational model of the experiment was developed and the uncertainty was evaluated for each step of the mathematical data processing. The computational model indicates that the uncertainty in the experimental results is sufficiently low to obtain meaningful results for the diffusive flux, at least for a case in which the vapor transport is mostly diffusive. We will be extending our uncertainty analysis to a case in which natural convection is the major component of the vapor transport, and if it can be shown that the uncertainty for this case is also sufficiently low, then our vapor distribution measurement technique can be a very valuable tool for learning about the vapor transport phenomena controlling evaporation.

Impact of the Research

This research program has a very large impact on the participating students. During the last year, four undergraduate students participated in the research and learned valuable lessons not only about the physical phenomena we are studying but, more importantly, about how to go about conducting research, i.e. how to think about problems, how to design and conduct experiments, and how to analyze measurement results. Three of the students devoted 10 weeks during the summer to the research and thereby gained an intensive research experience.

For the first principal investigator, this PRF supported research is his primary research focus and, therefore, is very important for his continuous development as a researcher and academician. Furthermore, the research has become a prime example of interdisciplinary work at our university, with faculty from Engineering Science, Chemistry, and Mathematics working together.