Reports: ND554513-ND5: Mechanics and Stability of Surface-Confined Assemblies
Gregory M. Grason, University of Massachusetts Amherst
Benjamin Davidovitch, University of Massachusetts
As a first step towards the long-term goal, a primary aim of the project is to study the structure and energetics of hexagonally-ordered sheets bound to spherical, yet deformable, substrates as a primitive model for capillary-mediated particle assemblies at liquid droplet interfaces. To this end, we are developing a combination of continuum elasticity and coarse-grained simulation approaches to investigate the structure and energetics of competing patterns of wrinkles and lattice dislocations that both relax stresses in circular sheets adhered to deformable sphere. Based on these models, we will relate the particle-sheet morphology to parameters that govern the overall shape and mechanics of the sheet, including the size and effective elasticity of the sheet, and shape, deformability and adhesive strength of the substrate (e.g. droplet), as well as further parameters that control the microscopic sheet behavior, such as bending stiffness and core size and energies of lattice defects. In later stages of the project, the model will be generalized to include the impact of cohesive inter-particle forces in regulating crack-formation and particle-desorption instabilities, as well as variations of surface geometry, including negatively-curved models of inter-droplet "necks".
In year 1 of this project, our efforts focused on: A) developing and implementing a coarse-grained simulation model of hexagonally-ordered sheets bound to deformable spheres; and B) developing a theoretical understanding of the wrinkling response of finite-thickness sheets bound to spheres in the limit of weak force at the sheet edge. In year 2, our efforts have been focused on pursuing part B. Combining analytic work with simplified (variational) numerical model, we developed a basic understanding of wrinkle patterns induced by rigid geometric constraints (e.g. an imposed spherical shape) rather than by tensile loads. To understand the significance of this finding, one should recall the basics of "tension-field theory" for very thin solid sheets. This classical theory results from the asymptotic limit of Foppl-van-Karman
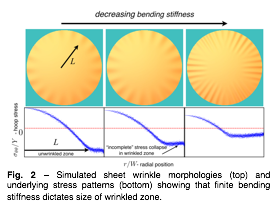
Fig. 2 – Simulated sheet wrinkle morphologies (top) and underlying stress patterns (bottom) showing that finite bending stiffness dictates size of wrinkled zone.
equations; it states that in the presence of tensile loads at the boundaries, a sufficiently thin sheet will develop a compression-free stress field, which is insensitive to any "fine structure" (e.g. the wavelength of wrinkles or curvature of folds), and is dictated only by the boundary loads, rather by the thickness. Our work lays out an analogous (but strictly distinct!) set of rules for a "tension field without tension" theory, which dictates the energy, stress, and morphology, in situations where a sheet is subjected to a geometric frustration (i.e. imposed Gaussian curvature), in the absence of tensile boundary loads. In such situations, our theory states that the hierarchical structure of energies is reversed with respect to classical tension field theory: (1) the dominant energy becomes associated with the fine structure of the pattern (not only with the average wavelength of wrinkles, but also with their spatial variation), which must be subjected to an "asymptotic isometry" constraint (i.e. negligibility of stress in comparison to bending, for sufficiently thin sheet). (2) Once the optimal fine structure is determined (which can be done with the aid of a "local-l-law" [Paulsen et al. PNAS 2016]), the residual stress is determined by a revised version of the classical tension field equations.
This new (and arguably counter-intuitive) set of rules was implement for the sheet-on-sphere problem, exhibiting an excellent and nontrivial agreement with direct numerical simulations. We believe that the importance of this discovery goes far beyond this simple model system, forming a basis to a new conceptual framework for studying elasticity of thin solid structures under geometric constraints.
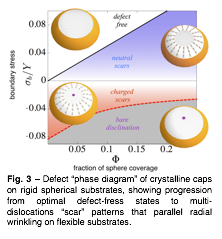
Fig. 3 – Defect Òphase diagramÓ of crystalline caps on rigid spherical substrates, showing progression from optimal defect-fress states to multi-dislocations ÒscarÓ patterns that parallel radial wrinkling on flexible substrates.
An additional effort of year 2 was to extend the principles of far-from threshold stress to crystalline caps bound to infinitely rigid spheres of increasing curvatures. It is known that increasing Gaussian curvature of a 2D crystal drives transitions to states possessing one or more 5-fold disclinations. Our study investigated the role of mutli-dislocation "scar" patterns in facilitating stress collapse in various regions of the sheet, dependent on the curvature, presesence of excess disclinations and external forces at the edge. Importantly, this theory shows that dislocation scars have the ability, unlike wrinkles or folds, to collapse regions of tension as well as compression, and finally, that the stable pattern is fully determined the tensile vs. compressive nature of the forces acting that the cap boundary. This work was published in Physical Review E this year.
The project involves the training of a Physics Ph.D. graduate student (Mr. Yiwei Sun), who is jointly advised by PIs Grason (Polymer Science and Engineering) and Davidovitch (Physics). Through this interdisciplinary research project, Mr. Sun learns a combination of techniques for soft materials modeling, including elasticity theory and geometry of crystalline sheets, simulation methods for multi-scale structures, and numerical optimization techniques. This project involves a collaboration with Prof. Rastko Sknepnek (University of Dundee) to develop new algorithms for physical processes of multi-scale structure relaxation in deformable membranes, to be ultimately incorporated into and distributed through a simulation package he is developing.