61st Annual Report on Research 2016

The goal of this research is to better understand the mechanism of bulk three- dimensional melting using computer simulations. When a system is in a crystalline state and is either heated or the pressure is lowered eventually the free energy of the liquid state becomes less than that of the crystal state and thus the liquid state becomes the thermodynamically stable state. In experimental situations most systems will melt starting at a surface or a defect such as a grain boundary. However, far from any surface with no defects the system will remain in a metastable crystalline state until eventually the free energy crystalline local minimum disappears. Our work is designed to explore what happens when the metastable crystal finally melts.

The usual way of discussing melting is in terms of nucleation theory, where one assumes that thermal fluctuations create local regions of liquid-like particles. The free energy of the liquid is lower than that of the crystal, but there is a free energy cost due to the surface between the liquid droplet and the crystalline matrix. The droplet radius can grow and shrink and when it grows past a critical radius then the droplet will grow to a macroscopic size and the system melts. This scenario does not seem evident in our simulations. Instead we see liquid like particles forming clusters of many sizes near melting and these clusters come and go rapidly. The distribution of liquid like particle clusters conforms to a size distribution consistent with random percolation theory. When the clusters merge to form a system wide cluster then the system can melt very quickly.

This year we focused on understanding what it means to be a liquid-like particle. We used three different definitions of liquid-like particles. The first considers  those particles whose root mean square deviation from their lattice sites exceeds a certain fraction of the lattice spacing to be liquid-like. We call this definition the Lindemann definition. The second definition uses the l=6 spherical harmonic, Y_lm. First Y_6m is averaged over all nearest neighbors of a particle to produce a quantity Q_6m for each particle. Then one constructs a rotationally invariant  quantity from Q_6m for all m_, which we call Q₆. If Q₆ is  less than a certain value then the particle is defined to be liquid-like. We call this threshold Q₆^*.  The third definition also uses the l=6 spherical harmonic, but considers the correlation between Q_6m of a particle with that of its nearest neighbor. If the correlation is less that a specific value c₁ for a certain number of neighbors c₂, then the particle is defined to be liquid-like. We find that all three definitions provide similar results even though the specific particles defined to be liquid-like by one definition are not necessarily the same as those defined by another definition.

Below we show the cluster distributions near melting for both Lennard-Jones and Yukawa potential Monte Carlo constant pressure simulations. For the Lennard-Jones simulations we start with a Face Centered Cubic lattice structure of 2048 particles, and for the Yukawa potential we start with a Body Centered Cubic lattice structure of 2000 particles.

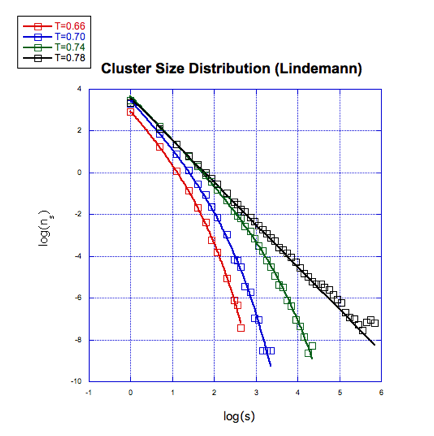
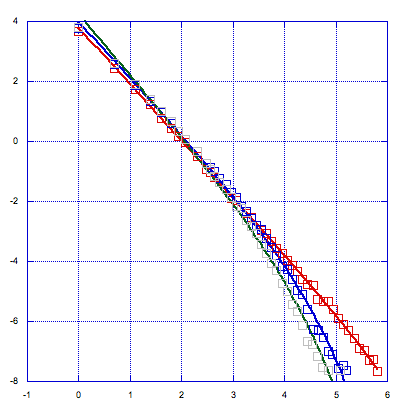
Figure 1(a)  Lennard-Jones potential, Lindemann threshold is 0.17.

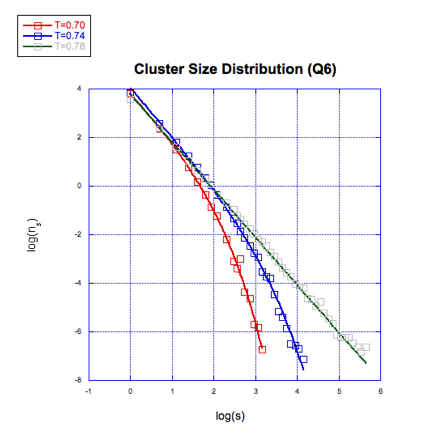
Figure 1(b)    Lennard-Jones potential,  Q₆ threshold is 0.34.

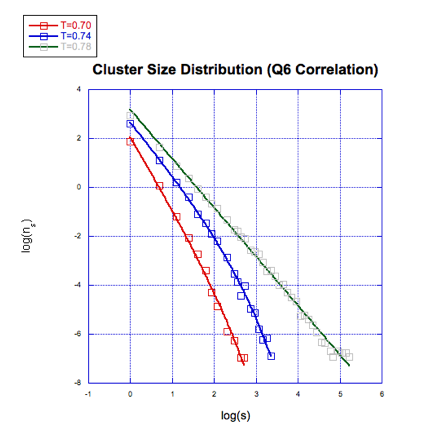
Figure 1(c)   Lennard-Jones potential,   Q₆ correlation c₁ = 0.65 and c₂ = 11.

Figure 1   The above three plots are for the Lennard-Jones potential: log-log plot of the size distribution of liquid-like particle clusters at various temperatures nearing transition. Each plot corresponds to a different criterion for liquid-like particles. The rightmost curve corresponds to the temperature closest to melting.  The temperature is in units of e /k, where e is the well depth of the Lennard–Jones potential and k is Boltzmann's constant. The simulations are done at constant pressure with a pressure equal to 0.

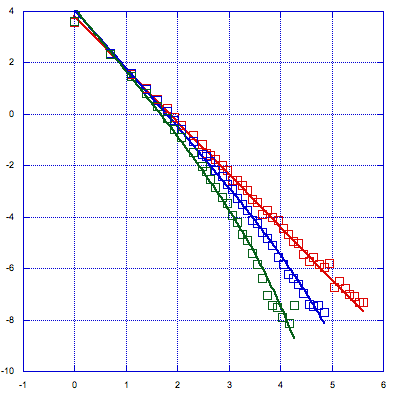
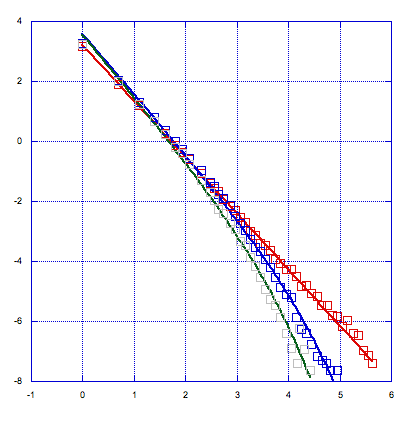
Figure 2(a)  Yukawa potential, Lindemann threshold = 0.26.

Figure 2(b) Yukawa potential, Q₆ threshold is 0.42.

Figure 2(c) Yukawa potential, Q₆ correlation  c₁ = 0.5 and c₂ = 7.

Figure 2   The above three plots are for the Yukawa potential V(r) = e^-r/r. Shown are log-log plot of the size distribution of liquid-like particle clusters at various temperatures nearing transition. Each plot corresponds to a different criterion for liquid-like particles. The rightmost curve corresponds to the pressure closest to melting. The temperature kT = 6.3 x 10^-4, where k is Boltzmann's constant. The three pressures shown from left to right are 5.3 x 10^-4, 5.1 x 10^-4 and 4.9 x 10^-4.

These cluster distribution plots all show the same general behavior, which is similar to those of a random percolation transition in three dimensions.  The various thresholds for the liquid-like definitions are determined such that the percolation transition occurs very close to where the system usually melts given enough time. We see the characteristic power law behavior at the threshold, with a critical exponent close to 2 consistent with the random percolation value of 2.19. Our work suggests that the mechanism of melting without any defects occurs from a percolation like transition where clusters of liquid-like particles of all sizes eventually form a cluster large enough to span most of the system. When this happens the system then rapidly melts. We have experimented with repeating simulations from the same configuration close to melting, but with different random numbers and have seen some cases where the system remains crystalline for a very long time and others where they melt. We expect our results may be related to behavior found in other systems near spinodals or pseudo-spinodals.

Four students worked on the project this past year, one sophomore over winter break, one student who finished early and worked in the spring before enetering graduated school in physics and two more students over the summer. This work is also has received attention from colleagues at Boston University who are likely to continue working on it with me.