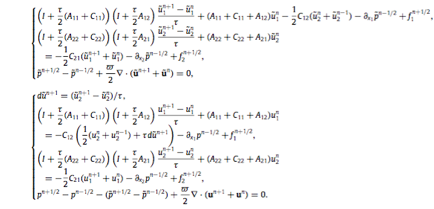61st Annual Report on Research 2016

Due to difficulties in hiring highly qualified personnel to work on this project, the actual work started in May 2016. The MSc student A. Prasetiyo had the task to modify an existing code for solution of the Navier-Stokes equations, based on the massively parallel algorithm proposed in Guermond and Minev (2011). Ari implemented a more accurate and efficient scheme proposed recently in Guermond and Minev (in press) that can be summarized as:

Here A₁₁, C_11, A₂₁ are second order derivatives in the x spatial direction, A₁₂, A₂₂, C₂₂ are derivatives in the y-direction, and C₁₂, C₂₁ are mixed second derivatives. This is a second order 2D scheme that has a straightforward extension to the 3D case as well. The code has been tested and verified. Currently we are working on the implementation of a level set, interface-capturing algorithm for solving free boundary problems. Proposed by Olsson and Kreiss (2005). The plan is to finalize the tests at the end of August 2016. I am also waiting for the arrival of a new postdoc that will greatly accelerate the work on the project. He was made an offer at the beginning of May 2016, however, due to a visa issue, has not started yet.

References:

J.L. Guermond and P. Minev, A new class of massively parallel direction splitting for the incompressible Navier-Stokes equations. Comp. Meth. Appl. Mech. Engng., 200 (2011), 2083-2093.

J.L. Guermond and P. Minev, High-order time stepping for the Navier-Stokes equations with minimal computational complexity. J. Computational and Applied Mathematics, in press.

E. Olsson, G. Kreiss, A conservative level set method for two phase flow, J. Comp. Phys., 210 (2005), 225-246.