Reports: UR455266-UR4: The Use of a Cyclopropylcarbinyl Radical Rearrangement as a Singlet Diradical Probe
Phyllis A. Leber, Franklin and Marshall College
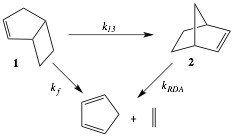
Bicyclo[3.2.0]hept-2-ene (1) undergoes thermal isomerization to norbornene (2) in the gas phase (Scheme 1). This rearrangement has served as a historical exemplar of a [1,3] sigmatropic carbon migration. Competitive isomerization and fragmentation processes at temperatures in excess of 300 oC convert 1 to its isomer 2 or directly to fragments cyclopentadiene and ethylene (Scheme 1).1,2 Determination of an accurate rate constant k13 for the [1,3] rearrangement of 1-to-2 and the associated Arrhenius parameters is complicated by the observation that 2 experiences facile Diels-Alder cycloreversion (retro Diels-Alder reaction) to cyclopentadiene and ethylene. Despite the large experimental error in activation parameters for the [1,3] process, Cock and Frey conclude that the activation parameters for the sum (k13 + kf) are close to the expected values 'if both processes have a biradical mechanism' and therefore that 'a two-step pathway is competitive.'
Scheme 1. Thermal Reactions of Bicyclo[3.2.0]hept-2-ene (1)
In a dramatic reversal of this mechanistic rationale, Woodward and Hoffmann declared emphatically that exo-7-d-endo-6-acetoxybicyclo[3.2.0]hept-2-ene 'undergoes a concerted symmetry-allowed suprafacial [1,3] shift, with inversion at the migrating center, É at 307 °C.' 3 According to the Woodward-Hoffmann rules, suprafacial migration with inversion of configuration (si) is privileged as orbital-symmetry allowed and suprafacial migration with retention of configuration (sr) is orbital-symmetry forbidden. The mechanistic debate about whether the [1,3] sigmatropic rearrangement is concerted or stepwise has therefore primarily focused on stereochemical outcomes in cases where the migrating center, C-7 of bicyclo[3.2.0]hept-2-ene, carries a substituent to enable differentiation between the si and sr products. Thus, si/sr ratios have been cited as a measure of the degree of orbital symmetry control in [1,3] sigmatropic rearrangements.
Our current mechanistic analysis is that [1,3] sigmatropic rearrangements traverse short-lived diradical transition structures residing on a shallow energy surface.7 The mixed stereochemical results that have often converged toward a value of unity have effectively subverted alternative mechanistic interpretations such as competing orbital symmetry-allowed (si) and orbital symmetry-forbidden (sr) pathways8 or competing concerted (si) and diradical (si/sr) mechanisms.9 The potential however for a short-lived nonequilibrated diradical intermediate to partition between inversion and retention modes10 deserves more critical examination.
The higher stereoselectivity observed for exo-7-methylbicyclo[3.2.0]hept-2-ene (3)2 versus that of deuterium-labeled 1 suggests that either steric factors or the moment of inertia about the C6-C7 bond might well influence the stereoselectivity of the [1,3] migration. It is this proposition that allowed us to reconsider our earlier assumption that all exo-7-alkylbicyclo[3.2.0]hept-2-enes would yield comparable results both kinetically and stereochemically.
The thermal reactions of the exo-7-alkylbicyclo[3.2.0]hept-2-enes were followed at 275 oC in the gas phase. The relative order of importance of kinetic processes is k13 > kf (Table 1) although the k13/kf ratio decreases as the alkyl group increases in size.
Capillary GC analysis provided relative concentration versus reaction time data for the reactants and for all isomeric products. A mixture of each exo- and endo-5-alkylnorbornene pair was also heated at 275 oC in order to obtain rates of the respective Diels-Alder cycloreversions. The rates of retro Diels-Alder reactions for all exo-5-alkylnorbornenes were comparable as were those for the endo-5-alkylnorbornenes. In all cases the reactivity of the endo-5-alkylnorbornenes exceeded that of the corresponding exo-5-alkylnorbornenes by a factor greater than 2 (Table 2).
Table 1. Rate Constants and Exit Channels for
exo-7-Alkylbicyclo[3.2.0]hept-2-enes
R-
| Rate Constant @ 275 ¼C
| krel | k13/kf | % [1,3]
| % epim
| % frag
|
Me- | 1.8 x 10-5 s-1 | 2.2 | 150 | 93 | 4 | 0.6 |
Et- | 1.6 x 10-5 s-1 | 2.0 | 11.5 | 92 | 0 | 8 |
i-pr- | 1.1 x 10-5 s-1 | 1.3 | 2.2 | 69 | 0 | 31 |
D- | 0.8 x 10-5 s-1 | 1 | 2.1 | 67 | 6 | 27 |
Table 2. Rates of Retro Diels-Alder Reactions for
exo- (k1,RDA) and endo- (k2,RDA)-7-Alkylbicyclo[3.2.0]hept-2-enes
R-
| k1,RDA | k2,RDA
| k1,RDA/ k2,RDA
|
Me- | 2.0 x 10-4 s-1
| 4.7 x 10-4 s-1
| 2.35 |
Et- | 2.2 x 10-4 s-1
| 5.6 x 10-4 s-1
| 2.54 |
i-pr- | 1.7 x 10-4 s-1
| 4.6 x 10-4 s-1
| 2.71 |
Our preliminary thermal studies suggest that changing the alkyl group on the migrating carbon C-7 has little impact on reaction rates but results in a correlation between the stereoselectivity of the [1,3] sigmatropic rearrangements of exo-7-alkylbicyclo-[3.2.0]hept-2-enes and the mass of the C-7 substituent. A linear relationship is also evident but less well-defined when the si/sr ratio is plotted versus either the respective Charton or Taft steric parameters. Currently, thermal reactions of other exo-7-alkylbicyclo[3.2.0]hept-2-enes are underway so we can extend this analysis to more analogs.
Katie Kidder, one of two F&M undergraduates support by PRF funds in the summer of 2016 conducted experimental synthetic work in my lab and also engaged in a computational study of some of the hydrocarbon reactants and products relevant to this current investigation. Prof. Alex Davis, who has been mentoring Katie in theoretical chemistry, has added a new dimension to our research by coupling computational and experimental analysis. Because Katie intends to pursue a Ph.D. in computational chemistry, this has and will continue to be an excellent research experience for her. We believe that the inclusion of computational analyses with our experimental data in a future publication will enhance the value of the research. Should these efforts be productive, Prof. Davis and I might well establish a permanent research collaboration.
[1] H. M. Frey, A. T. Cocks, J. Chem. Soc. A 1971, 2564-2566.
[2] J. D. Bender, P. A. Leber, R. R. Lirio, R. S. Smith, J. Org. Chem. 2000, 65, 5396-5402.
[3] R. B. Woodward, R. Hoffmann, The Conservation of Orbital Symmetry, Verlag Chemie: Weinheim, 1970, pp 119-122.
[4] J. J. Gajewski, Acc. Chem. Res. 1980, 13, 142-148.
[5] J. A. Berson, G. L. Nelson, J. Am. Chem. Soc. 1967, 89, 5503-5504.
[6] P. A. Leber, J. E. Baldwin, Acc. Chem. Res. 2002, 35, 279-287.
[7] J. E. Baldwin, P. A. Leber, Org. Biomol. Chem. 2008, 6, 36-47.
[8] J. A. Berson, Acc. Chem. Res. 1972, 5, 406-414.
[9] G.-G. KlŠrner, R. Drewes, D. Hasselmann, J. Am. Chem. Soc. 1988, 110, 297-298.
[10] J. E. Baldwin, K. D. Belfield, J. Am. Chem. Soc. 1988, 110, 296-297.