61st Annual Report on Research 2016

The activities have involved a combination of analytical, experimental and computational tasks.

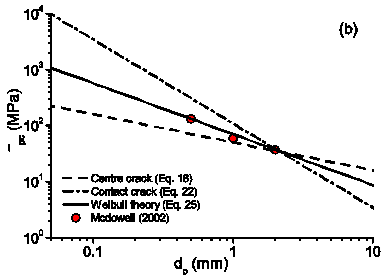
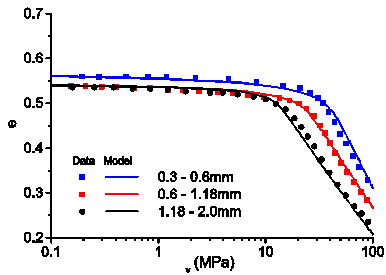
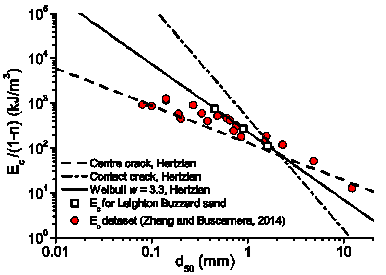
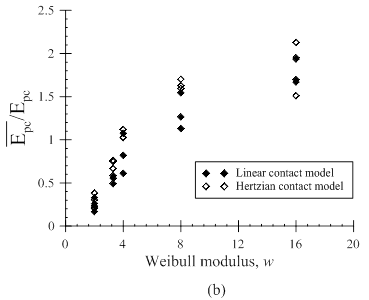
The analytical tasks have been aimed at formulating multi-scale models of grain crushing by taking into account the behavior of single grains, as well as the collective response of particles packed in an assembly. An upscaling law has been formulated to bridge the micromechanics of grain fracture with the yielding of granular soils. The model relies on a linear scaling between the energy required to fracture individual grains and the energy associated with the crushing of an assembly made of particles with the same characteristics. Several grain-scale models of contact deformation and grain fracture have been used to validate such hypothesis (Fig. 1). The strategy has been validated against data for various sands that displayed significant grainsize effects in terms of both particle- and continuum-scale properties. It has been shown that the combination of the Weibull’s statistics for particle strength with the Hertzian contact theory provides the best performance in predicting the effect of the grainsize on various indicators of particle failure, spanning from the tensile strength of the grains to the critical energy thresholds at the onset of fracture (Fig. 2). In addition, it has been shown that such combination of particle scale models is able to predict the effect of the grainsize in terms of yielding pressure, which for the case of quartz was captured satisfactorily by using data about the size dependence of the particle strength (Fig. 3). Furthermore, a comparison of the predictions from deterministic and statistical models has indicated that the data scatter can be explained in statistical terms, with the range of variation of the two deterministic theories being covered by values of Weibull moduli spanning between 2 and 6. This integration of breakage and fracture mechanics opens new avenues to estimate the effect of widely variable particle sizes in applications where the direct testing is not feasible, such as rockfill engineering, mining technology and petrophysical characterization of reservoir rocks.

Computational and experimental tasks have been aimed at validating the hypotheses of the theory.

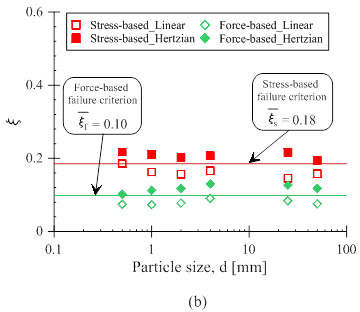
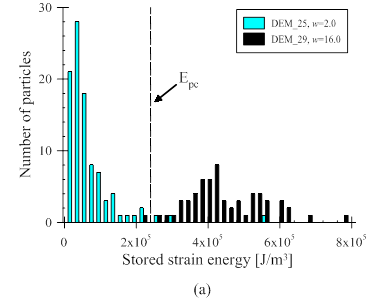
Numerical simulations based on the Discrete Element Method (DEM) have been performed to investigate the validity of the scaling laws linking the macro-scale yielding of an assembly to the fracture strength of single particles. The results of the simulations have been examined by energy scaling arguments, using both force- and stress-limiting failure thresholds (Fig. 4). The same contact and failure models used in the analytical task have been adopted. The simulated compression tests have confirmed that the energy input at the onset of comminution in an assembly scales linearly with the energy required to fracture single particles (Fig. 5). While the energy scaling constants have been found to depend on the variability of the particle strength (i.e., by finding considerable differences between deterministic and probabilistic failure models), they have also been found to fall in a narrow range. As a result, it has been shown that their values can be conveniently used in combination with a continuum theory such as the Breakage Mechanics to obtain satisfactory estimate of the size-dependence of the yielding pressure. Further analyses of the simulated comminution process have been done to study the effect of the particle strength variability. It was show that the statistical variability affects both yielding stresses and scaling factors, as well as that the largest departures between deterministic and probabilistic models occurs for low values of Weibull modulus, w (Fig. 6). These results corroborate the hypothesis that energy-scaling arguments are a valid approach to connect the macroscopic compression of granular materials with the fracture properties of their constituting particles, suggesting that satisfactory upscaling criteria must account not only for the energetics of crushing, but also for the variability of the grain-scale fracture properties.

A stage of laboratory experiments is currently underway. The experiments have been designed to test the hypotheses of the model about the influence of particle characteristics such as contact shape and particle angularity. The experiments will be based on two end members of granular material, i.e. spherical glass beads and highly angular quartz sand. Such experiments will be conducted through a new miniature compression device and a high-capacity loading frame equipped with radially rigid compression cells, which will be used for single particle compression and packing compaction experiments, respectively.

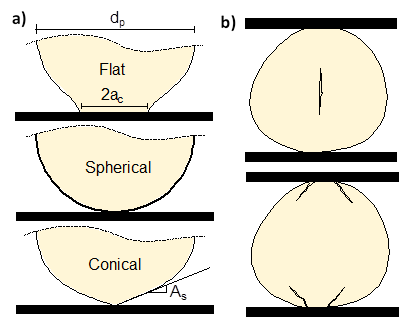
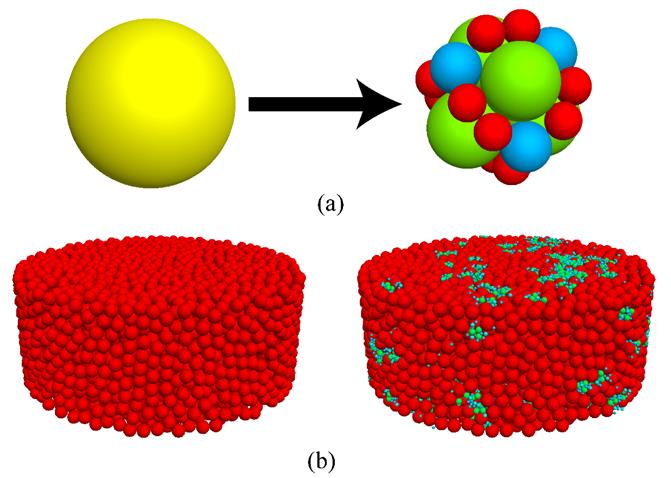
Fig. 1: Schematics of (a) contact laws (linear contact, Hertzian contact and conical) and (b) fractures models used for this project (fracture at the center of a particle or at the edge of a contact).

Fig. 2: Predicted grain size effect for (a) silica sand with grain size of (0.25-0.3)mm, (0.6-0.71)mm and (1.4-1.7)mm; (b) Leighton Buzzard sand grains.

Fig. 3: a) Measured vs. predicted 1D compression responses of Leighton Buzzard sand; b) Crushing energy at sample scale computed for three models.

Figure 4. (a) Illustration of the simulated particle breakage mechanism; (b) DEM specimen before and after oedometric compression simulation. The color of the particles reflects their size.

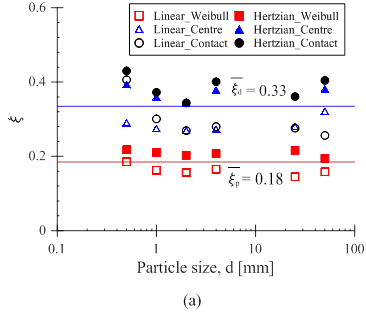
Figure 5. (a) Variation of the computed values of the scaling factor for 1D compression simulations on granular specimens; (b) comparison of the scaling factor values obtained using force- and stress-based failure criteria.

Figure 6. (a) Statistical distribution of the stored strain energy of fractured particles at yielding. The vertical dashed line indicates the energy required to fracture a single particle under diametrical compression; (b) influence of Weibull modulus w on the ratio between average particle fracture energy of the particles in an assembly and and the energy at the onset of single particle failure upon diametrical compression.