print pageprinter friendly
Reports: UR955347-UR9: Computational Studies of Osmotic Membranes for Petroleum Wastewater Reclamation

Mingheng Li, PhD, California State Polytechnic University

One of the main objectives of this research is to investigate the fundamental transport phenomena (including hydrodynamics and mass transfer) in industrial RO feed channels. Because the retentate flow may reduce by 50–60% in one pressure vessel, it is essential to establish the intrinsic relationship between pressure drop and average longitudinal velocity under industrial operating conditions. The overall pressure drop can then be calculated by numerical integration once this relationship is determined.   The strategy implemented was to simulate a widely used commercial RO element with detailed spacer geometry using Computational Fluid Dynamics (CFD). Additionally, an open channel simulation was made for comparison to elucidate the effect of the spacer filaments. A small fraction of the RO element was simulated and is shown in Fig. 1. Since the recovery in this computational domain is only about 0.2%, the average longitudinal velocity may be considered constant. By varying average longitudinal velocity at the inlet of the computational domain in the range of 0.1–0.25 m/s, it is possible to capture pressure drop characteristics at various locations of the pressure vessel under plant operating conditions.   The contours of velocity magnitude on eight yz slices of the computational domain as well as streamlines using the average interstitial velocity 0.25 m/s in the spacer-filled channel is shown in Fig 1(a). The plots for the unobstructed channel using average feed velocity 0.25 m/s are shown in Fig 1(b) for a comparison. Without the spacer, the streamlines are straight. This is because the velocity components in both y and z directions are minimal. With the presence of the spacer, the flow is forced to make turns around it, leading to a wavy and pseudo-periodic pattern. The maximum of velocity magnitude appears to be much higher even though the two domains have comparable average feed velocities. The y-component velocity could boost the velocity parallel to the walls. According to the boundary layer theory, the thickness of viscous boundary layer reduces as bulk velocity parallel to the surface increases. This in turn affects the diffusive boundary layer, reducing the effect of concentration polarization.  

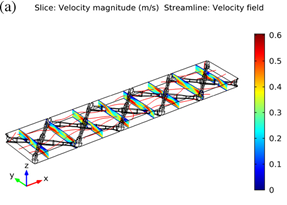
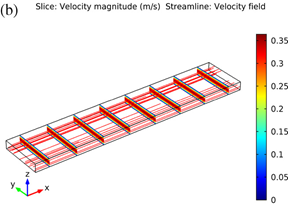
Fig. 1. Contours of velocity magnitude on eight yz-slices and streamlines in (a) spacer-filled channel and (b) unobstructed channel.   Another noticeable difference between both channels is that the spacer-filled channel has rolling cells on the yz planes. These recirculation zones are illustrated using streamlines on three yz planes, as shown in Fig. 2. Salt mixing would be promoted in these regions.  

Fig. 2. Streamlines (v, w) on three yz-slices in spacer-filled channel. The slices are cut at x =1/2, 11/20, and 3/5 of the length of the computational domain.   The pressure drop is significantly higher in the spacer-filled channel. It appears that the obstruction of spacer filaments contributes more to flow resistance as compared to the membrane walls.


Fig. 3. Pressure differential along feed direction with average feed velocity of 0.25 m/s. The x-axis is a horizontal line cut at y = 1/4 width and z = 1/2 of the computational domain.

In industrial BWRO operation, the average longitudinal velocity of the retentate stream gradually reduces as it travels along the pressure vessel due to water recovery. To develop a system level model for pressure drop, a parametric analysis is carried out by varying velocity at the inlet of the computational domain. The pressure differential is recorded and compared with correlations of channel flow. The Darcy friction coefficient is calculated as follows:

 

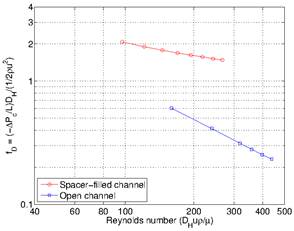
(1)

In the flat narrow channel the 3D numerical simulation matches closely with the theoretically derived relationship fD=96/Re. However, in the spacer-filled channel, fD is several times larger if the Reynolds number is the same.

Fig. 4. Darcy friction coefficient vs Reynolds number.

.

It is found that in the spacer-filled channel , or .

Salt concentrations and flow arrows are plotted on an xz plane for both the spacer-filled and unobstructed channels, as shown in Fig. 5(a). It is observed that concentrated islands are isolated in zones near the spacer filaments, where the flow is stagnant. These are areas associated with smaller fluxes. The concentrated region is thinner in regions with high fluid velocities. The concentration polarization profile in spacer-filled channel differs from the one in the empty channel, where a concentrated layer gradually develops along the channel severely reducing permeation flux.

Fig. 5. Salt concentration with fluid flow arrows on xz plane of (a) spacer-filled channel and (b) unobstructed channel.

The mass transfer coefficient km is related to salt concentration gradient at the membrane wall by the following equation:

 

(2)

Using the concentration gradients reported by the converged CFD solution and Eq. 2, the local mass transfer coefficients in the computational domain based on four different values of inlet velocities are calculated. This is because as water permeates through the membrane, the average longitudinal velocity decreases in a long pressure vessel, leading to a reduction in km. It is seen that km reduces with respect to both location and longitudinal velocity in open channel. For the spacer-filled channel, km reduces mostly with respect to longitudinal velocity. However, at a given velocity, it appears that km profile is repeated from cell to cell and there is no significant decay in cell-average km with respect to location.

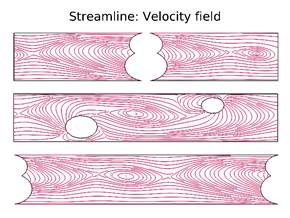
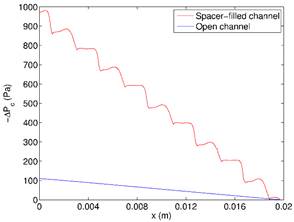
The cell-average km over the length of five unit cells is calculated and it plotted as a function of  on a loglog scale, as showed in Fig. 6. Both follow straight lines, however, the slopes and magnitudes are different. In the open channel, ; the power law index is very close to 1/3 as indicated by the boundary layer theory. In the spacer-filled channel, . The existence of spacer filaments significantly enhances mass transfer.

 

     
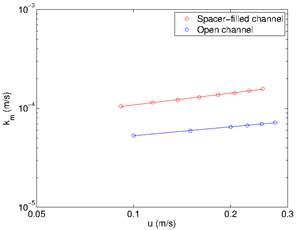
Fig. 6. Cell-average km as a function of average feed velocity.