61st Annual Report on Research 2016

Adsorbed species on solid surfaces are involved in many reactions of great technological importance, especially in catalysis, electrocatalysis, and fabrication of microelectronics and photovoltaics. As such, there has been tremendous effort worldwide to learn how to predict reaction rates and equilibrium constants for elementary reactions involving adsorbates. Theoretical calculations of rate constants and equilibrium constants for such reactions require knowing both the enthalpy and entropy of the adsorbed species and transition states. While much effort has been devoted to measuring and calculating the enthalpies of well-defined adsorbates^1,2, few measurements of the entropies of adsorbates have been reported until our 2012 paper³ where we determined the entropies of a large number of adsorbed molecules. We combined those results with many previously-measured entropies to show that the entropies of adsorbed molecules are generally ~2/3 of that for the gas at 1 bar and the same temperature³. This is much larger than most theoretical predictions, which assume a lattice-gas model and use the harmonic oscillator approximation to estimate partition functions³. We have developed a new theoretical method for estimating entropies of adsorbed species that is much more accurate yet still quite easy to implement. This work has led to two papers, one describing the derivation⁴ and another its implementation ⁵. These will be very useful to future researchers in catalysis since it provides much more accurate predictions of equilibrium constants for surface reactions and kinetic prefactors than the standard harmonic oscillator approximation.

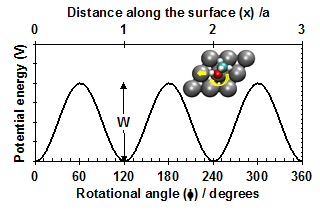
Previously, surface chemists had usually thought of adsorbate entropies in terms of the two limiting cases discussed in statistical thermodynamics texts: the 2D lattice gas model and the 2D ideal gas model ⁶. In calculating rate constants for surface reactions based on quantum mechanical calculations (mainly density functional theory, DFT) of reactant and transition state energies, surface chemists almost exclusively rely on harmonic transition state theory approaches, which assume that each adsorbate is a localized oscillator with only vibrational modes^7-11. This misses the fact that translations and rotations of adsorbates parallel to the surface are actually much more labile, and hence greatly underestimates entropies. Our new method accurately considers the nature of the potential energy surface for these motions, which have small but significant periodic barriers to motion. The translational barrier is repeated every lattice constant (a), and the periodicity of the rotational barriers is determined by the surface symmetry, as in Fig. 1. In principle, one must solve the Schrödinger Equation for this potential to get the quantum-mechanically allowed energy levels, and then sum over these states to get the partition function, q.

To do this, we utilized an approximation similar to that originally developed by Pitzer and Gwinn¹² and improved by Goddard’s group ¹³, and widely used for calculating partition functions of hindered rotors within gas molecules. We used DFT with periodic boundary conditions and the nudged elastic band method to estimate rotational and translational barrier heights and their periodicities. A few model systems with widely varying physical properties were studied, to learn how differences between systems qualitatively affect entropies and kinetic prefactors for adsorbates ⁵.

In doing this, we realized that the statistical mechanical framework for treating adsorbates as hindered translators had never been fully developed, nor could we find any treatment of chemical reaction equilibria at the partition-function level for adsorbate reactions wherein adsorbates were treated with both the ideal lattice gas and the ideal 2D gas approximations within the same equilibrium constant. Starting from the very first principle equations involving chemical potentials we derived a self-consistent set of equations for calculating equilibrium constants for such cases, and extended it to also simultaneously include adsorbates treated as hindered translators⁴. We further extended those to derive equations based on transition state theory for the rate constants and prefactors for chemical reactions involving adsorbates which mix all three classes of adsorbate models⁴. These results should be useful for future researchers modeling surface reaction kinetics.

Educational Benefits

This work is in collaboration with Dr. Líney Árnadóttir, a new Assistant Professor at Oregon State University. It provides research-based outreach to a small regional university, and guidance for the early-career development of this promising young female investigator. The funding has partially paid for three students in her group, thus helping her build up her research program. This is my first grant for purely theoretical research, thus adding a new component to my group.

References:

(1) Campbell, C. T.; Lytken, O. Surface Science 2009, 603, 1365,

(2) Brown, W. A.; Kose, R.; King, D. A. Chem. Rev. 1998, 98, 797,

(3) Campbell, C. T.; Sellers, J. R. V. Journal of the American Chemical Society 2012, 134, 18109,

(4) Campbell, C. T.; Sprowl, L. H.; Arnadottir, L. Journal of Physical Chemistry C 2016, 120, 10283,

(5) Sprowl, L. H.; Campbell, C. T.; Arnadottir, L. Journal of Physical Chemistry C 2016, 120, 9719,

(6) Hill, T. L. An Introduction to Statistical Thermodynamics; Addison-Wesley: Reading, MA, 1960.

(7) Reuter, K.; Frenkel, D.; Scheffler, M. Phys. Rev. Lett. 2004, 93, Art. #116105,

(8) Gokhale, A. A.; Kandoi, S.; Greeley, J. P.; Mavrikakis, M.; Dumesic, J. A. Chemical Engineering Science 2004, 59, 4679,

(9) Honkala, K.; Hellman, A.; Remediakis, I. N.; Logadottir, A.; Carlsson, A.; Dahl, S.; Christensen, C. H.; Norskov, J. K. Science 2005, 307, 555,

(10) Reuter, K.; Scheffler, M. Physical Review B 2006, 73, 045433.

(11) Gokhale, A. A.; Dumesic, J. A.; Mavrikakis, M. Journal of the American Chemical Society 2008, 130, 1402,

(12) Pitzer, K. S.; Gwinn, W. D. Journal of Chemical Physics 1942, 10, 428,

(13) McClurg, R. B.; Flagan, R. C.; Goddard, W. A. Journal of Chemical Physics 1997, 106, 6675,

Figure 1.Example potential energy surface for adsorbate motions parallel to the surface: translation (top axis), rotation (bottom).