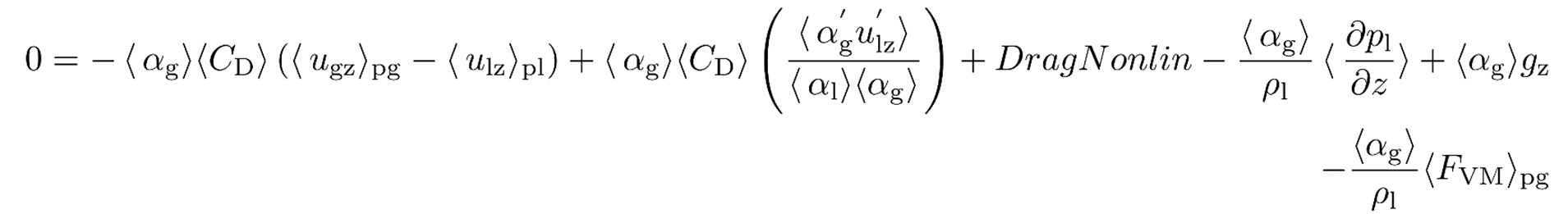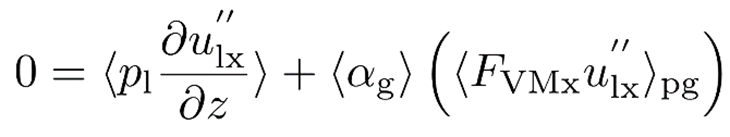61st Annual Report on Research 2016

Objective of the research

The main objective of the project is to investigate the turbulence mechanisms and interactions involved in dispersed gas-liquid flows through meso-scale direct numerical simulations (DNS) and develop more general turbulence models from the simulation data to improve the predictive capability of current CFD models employed for these flows. 

Computational setup

The computational domain for meso-scale DNS is constituted by a 3D box with a cross section of 0.15 x 0.15 m and 0.4 m tall. Periodic boundary conditions are applied on all sides of the box to eliminate the transport terms in the mean momentum and Reynolds Stress Transport (RST) equations and study only the influence of inter-phase force terms (drag, virtual mass, lift, buoyancy and bubble dispersion) on turbulence production. An air-water system is used as reference. The behavior of turbulence in the gas-liquid system is studied for different volume fractions (0.15, 0.2, 0.3, 0.4 and 0.5). The simulations indicate that the flow is stable for volume fractions below 30% and there is onset of turbulent instability for volume fractions above 30%.

Integral length scales

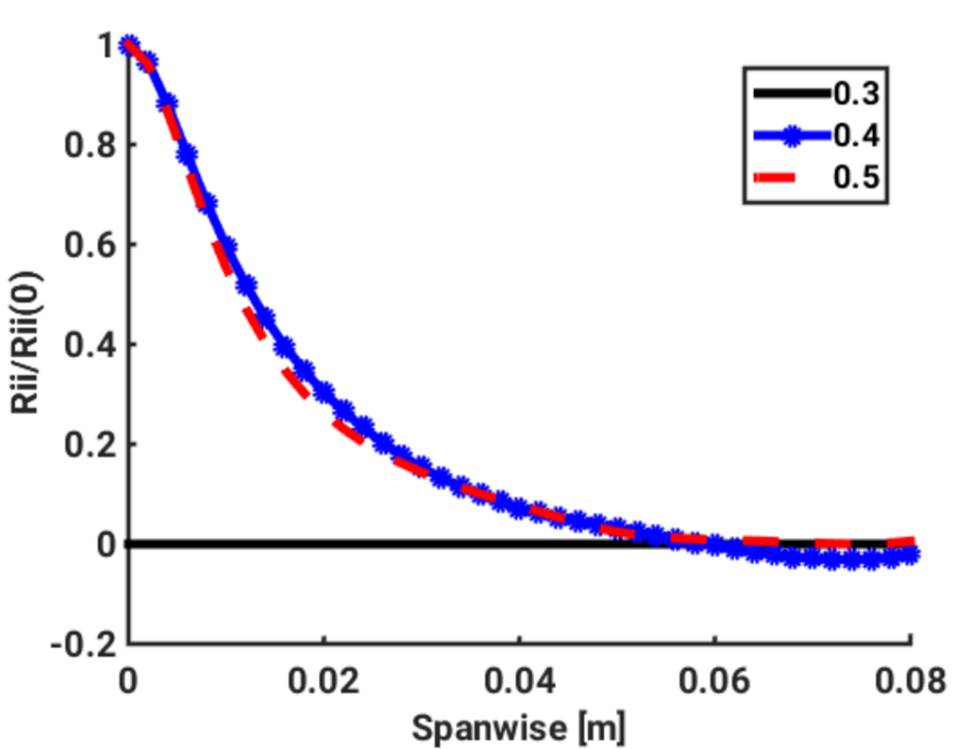
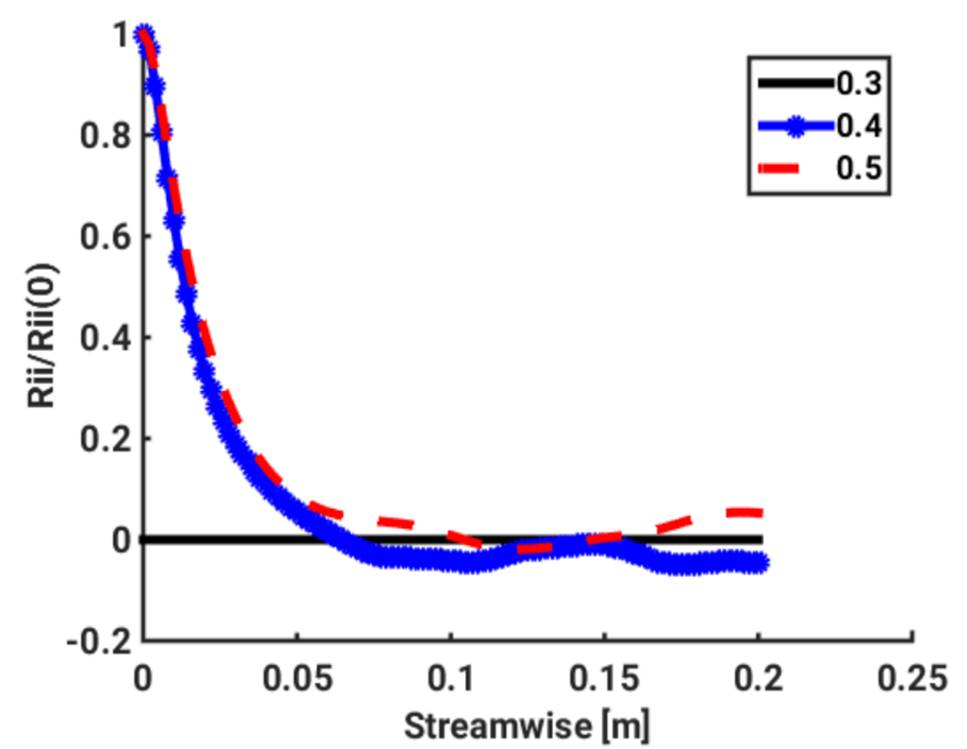
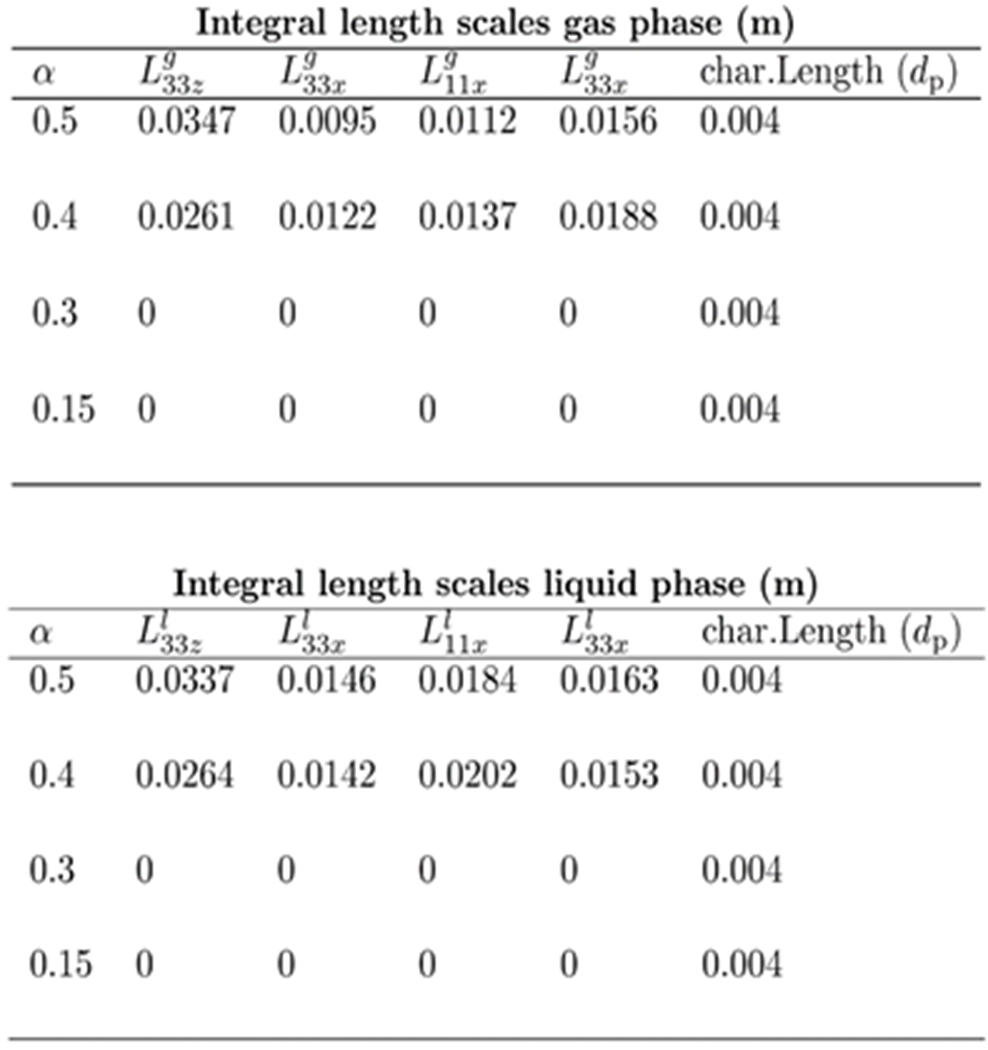
Integral length and time scales can be computed from the pair correlations functions in Figure 1 and 2.  It can be concluded from the tables that the integral length scale in the flow direction is larger than the integral scale computed in the direction perpendicular to the flow for both phases, this is due to the action of inter-phase forces preferentially acting in the flow direction compared to the other direction.

Moreover, the integral length scales for gas and liquid phase are similar indicating that the bubble follows the liquid due to low inertia. The length scales for volume fraction 30% and 15% is 0 due to no turbulence.

Figure 1: Pair correlation for the liquid phase in the spanwise direction.

Figure 2: Pair correlation function for the liquid phase in streamwise direction.

Mean momentum Equation in stream-wise direction

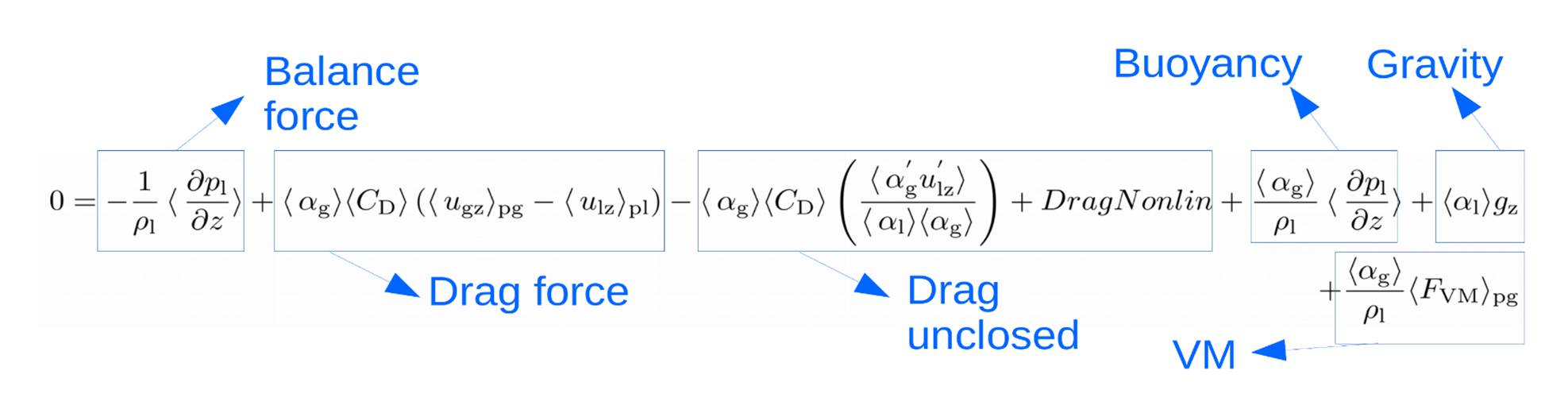
The phase momentum equation is simplified for a periodic box due to the periodicity of the system. The resulting momentum equations are given below for each phase.

Liquid-phase

The first term on the RHS of the equation is the forcing term used to balance the weight of the fluid mixture to avoid that the system continues to accelerate due to the effect of gravity in the periodic numerical setup.

Gas-phase

Momentum budget for different gas fractions

The gas-phase momentum budgets for both volume fractions indicate that the correlation (Drag unclosed) due to the Reynolds averaging of drag is positive and leads to drag reduction compared to the case of homogenous rise of bubbles. The value of correlations due to buoyancy force has negligible effect on the momentum. The correlations associated with lift force (Lift) and Bubble dispersion force (BD) due the statistical homogeneity (mean gradients of volume fraction and velocity are 0) of the flow. Correlations are null for the cases with volume fractions equal to 15% and 30% due to the absence of turbulence.

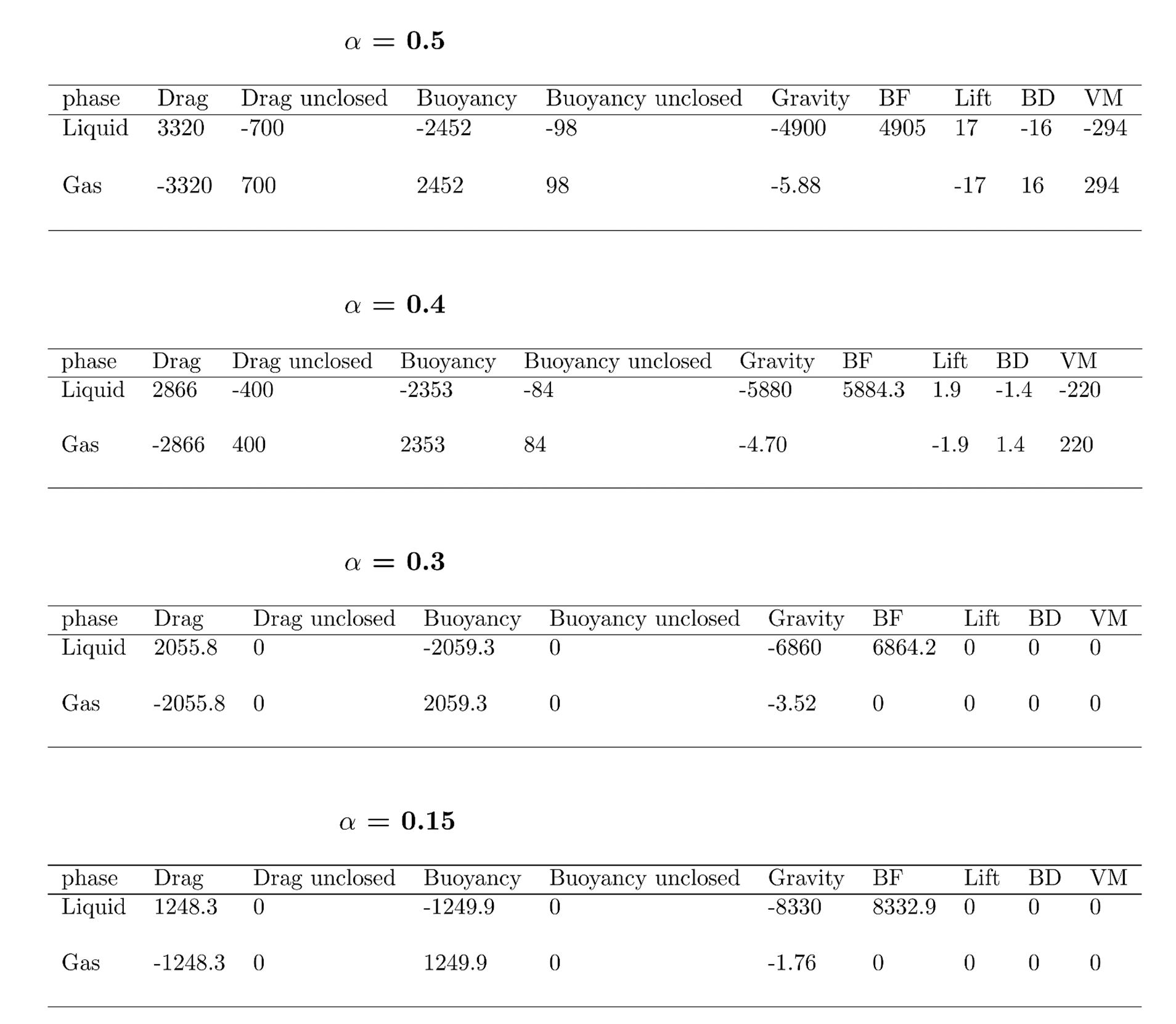
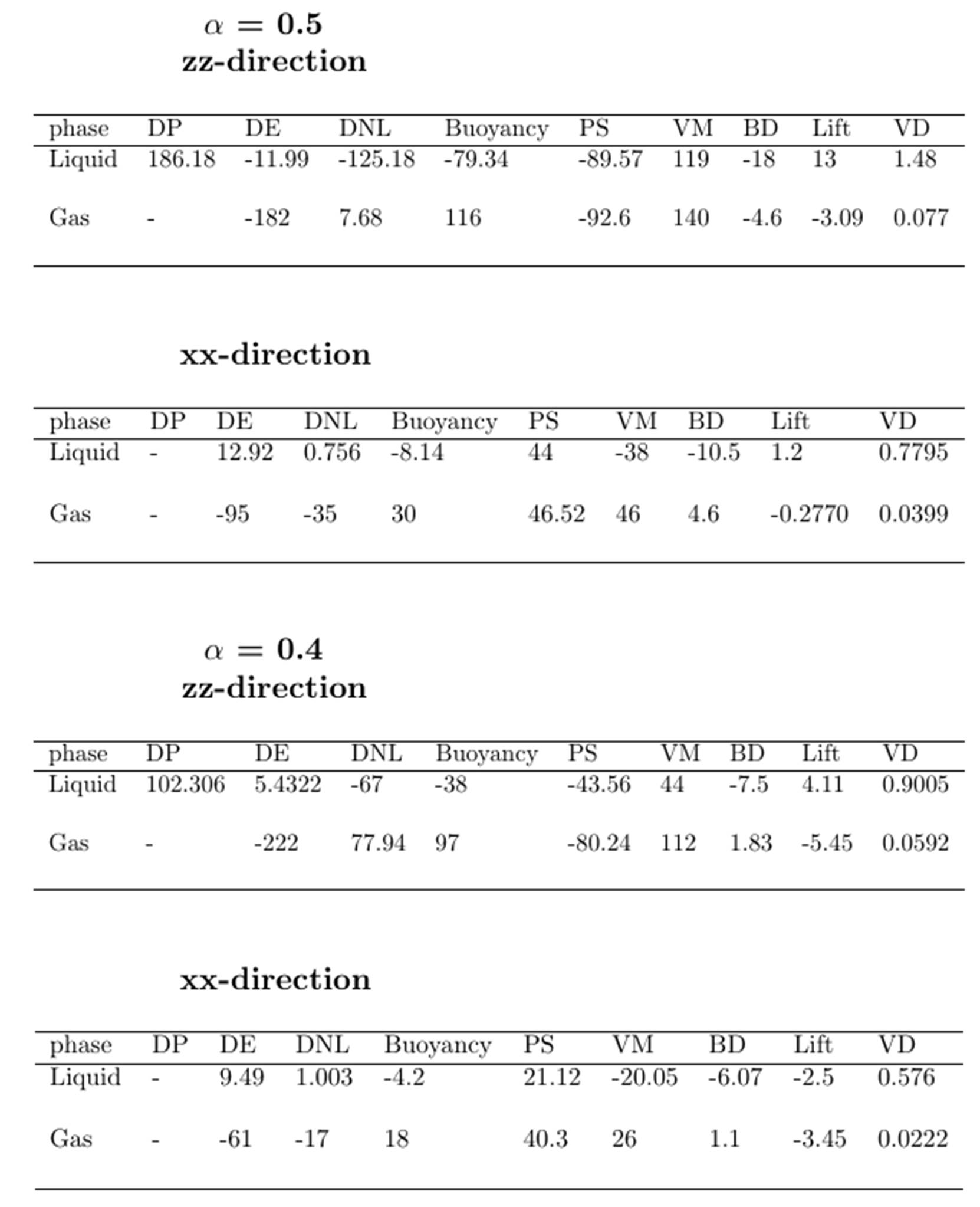
Reynolds stress transport equations and budget for a periodic box for volume fractions 0.4 and 0.5

Liquid-phase

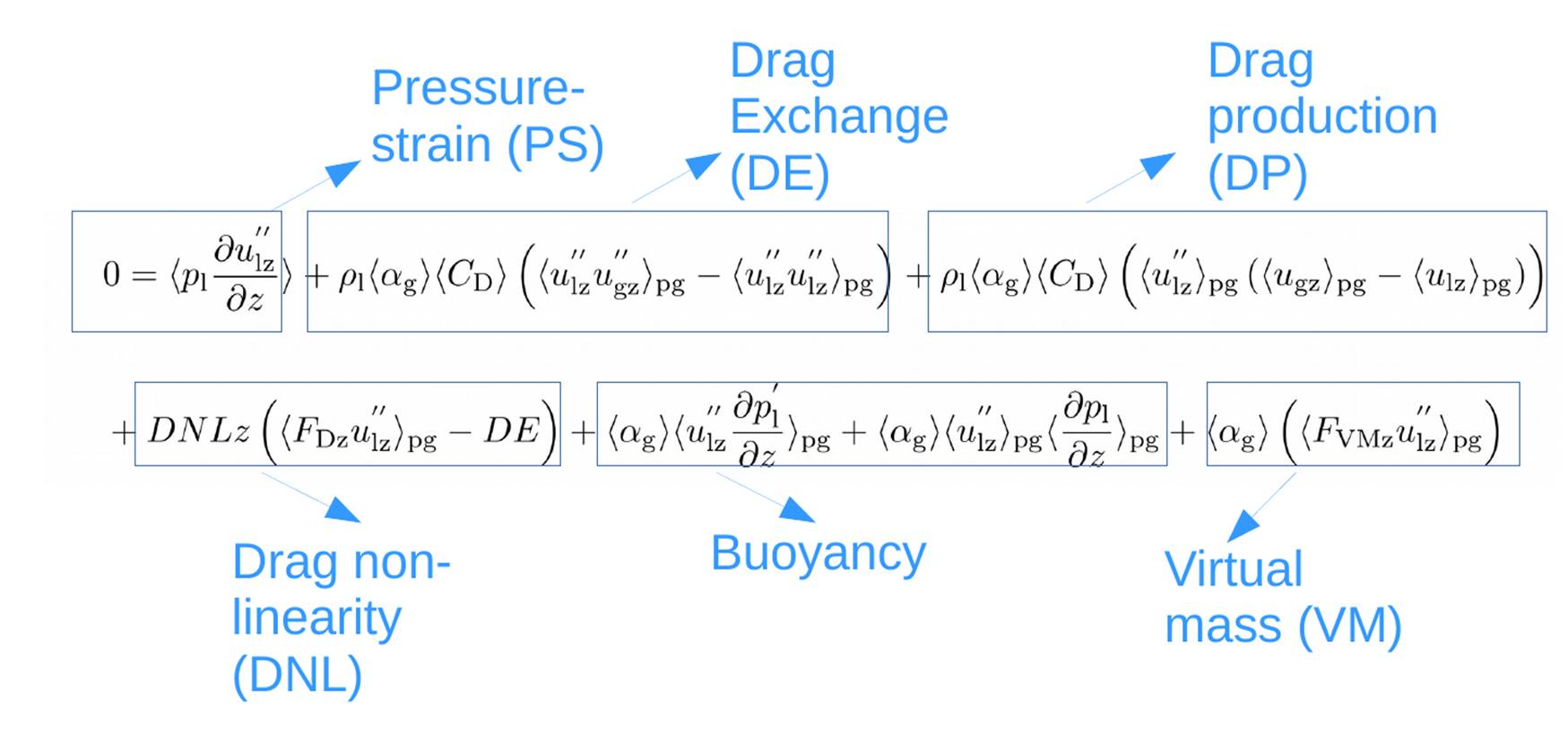
zz-direction

xx-direction

From the tables, it can be seen that the contributions of bubble dispersion (BD) and lift forces (Lift) are statistically insignificant due to the homogeneity of the flow. The main inter-phase forces which sustain the turbulence in the liquid-phase are drag and virtual mass due to the strong correlation of gas fraction fluctuation and liquid velocity. However, turbulence production in the gas-phase is mainly due to buoyancy and virtual mass. Since we do not perform a fully resolved DNS, the contribution of dissipative scales appear as negative contributions of the inter-phase forces, thus the contribution due to drag non-linearity (DNL) and buoyancy can be considered as dissipation of turbulent energy in the liquid-phase. The large values of the contributions of inter-phase forces towards the Reynolds stress in the zz-direction compared to xx-direction for both gas fractions shows the degree of turbulent anisotropy to be very high. This justifies the need for anisotropic turbulence models, which describe contributions from drag, buoyancy, virtual mass and pressure-strain terms for both the phases.

In the remainder of the project, the data obtained through meso-scale DNS will be used to model the terms unclosed terms appearing from the Reynolds averaging process, and the corresponding models will be validated to verify their accuracy in reproducing the results of direct numerical simulations.