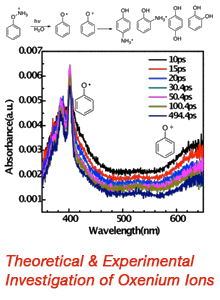
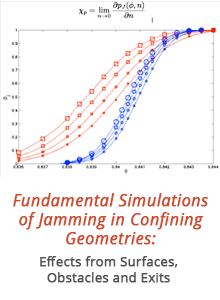
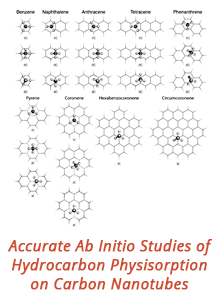
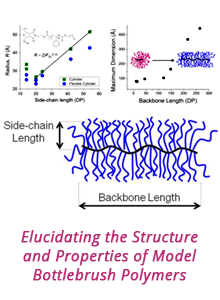
58th Annual Report on Research 2013 Under Sponsorship of the ACS Petroleum Research Fund

Under funding from this grant we have achieved major achievements in understanding the jamming transition, granular flows and the glass transition.

For reason of space I do not report on the glass transition here. This work has led to publications in peered-review journals with high standards: two manuscripts were published in Proceedings of the National Academy of Sciences, one in Physical Review letters, two in Soft Matter, and three papers are under review. Our two main achievements are as follows:

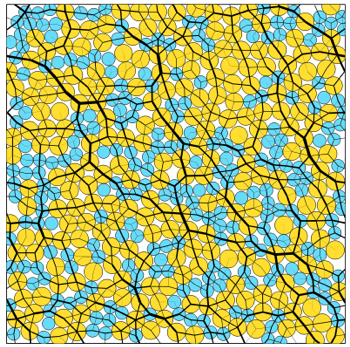
Fig.1 Computer simulation: Snapshot of a suspension of hard particles under flow (small particles are blue and large are yellow). The thickness of the black lines scales with the amplitude of the contact forces between particles.

Rheology of dense non-Brownian suspensions: rheological properties of dilute suspensions are well known since the early works of Einstein and Batchelor. Their behavior in the dense limit remains mystifying however, and of critical importance for the industry: it is central to the manufacture of materials and their applications, and to the understanding of slurries and oil sand. As the packing fraction of particles increases, particle motion becomes more collective, leading to a growing length scale and scaling properties in the rheology as the material approaches the jamming transition. There was a knowledge gap on this question, and no convincing microscopic description of this phenomenon. One the other hand, in recent years it had been understood that the elasticity of simple amorphous solids was governed by a critical point, the unjamming transition where the pressure vanishes, and where elastic properties display scaling and a diverging length scale. The correspondence between these two transitions was however unclear. Under ACS-PRF funding we established a formal analogy between the rheology of the flow and the elasticity of simple networks. This analogy led to a new conceptual framework to relate microscopic structure to rheology in flow. It enabled us to define and compute numerically normal modes and a density of states- quantities that are extremely useful to understand solid but that were overlooked to characterize flowing systems. Numerically the analysis of these modes in flow showed that at high density the system self-organizes into configurations that are extremely dissipative- much more than what one would naively expect. Fig.1 illustrates this analogy: one observes the contact force network generated between moving particles in flow, which is very similar to force chains observed in static granular packings.

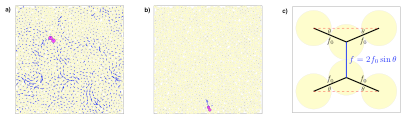
Non-linear excitations in granular materials: To understand theoretically the self-organization in flow and build a microscopic description of dense suspensions, we needed to understand the solid phase better. A fundamental question that was not addressed in the pasts was the nature of the non-linear excitations that appear in granular packings. For soft particles, these excitations are local rearrangements that induce to a quadripolar stress field, the so-called Shear Transformation Zone. We discovered a novel type of excitations in granular packings of frictionless particles, associated to the rewiring of the contact network. These excitations can be extended in space, but are associated with the opening of one contact carrying low forces. I showed that the stability of these excitations yields bounds on some exponents characterizing the distribution of forces P(f) and the pair distribution function g(r); showing that despite the considerable theoretical literature on these questions, rethinking them was necessary. The saturation of these bounds is necessary to explain power-law avalanches of plasticity seen in packings. With E.Lerner and G.During, post-docs in the group, we worked out these predictions fully and confirmed them numerically, showing that the system is marginally stable toward non-linear excitations. A similar situation occurs in other glasses (electronic and mean-field spin glasses), where marginal stability also causes broadly distributed avalanches.

Examples of two non-linear excitations in packings. They correspond to displacement fields resulting from pushing apart a pair of particles carrying a weak contact force, represented as shaded. Panel (a) exemplies the case where the displacements of the rest of the particles are of the same order of the displacements of the pushed pair. Panel (b) displays a different displacement field generated in the same conguration as in panel (a) by pushing apart a different pair of particles. This time the pushed pair's displacement is signicantly larger than the displacements in the rest of the system. Such contacts are very weakly coupled to external stresses applied on the boundary, i.e. they are mechanically isolated. Panel (c) displays a local configuration of particles that gives rise to small displacements when opening the vertical contact

Overall, we have developed a novel framework to understand granular solids, together with the flow of dense suspensions. There is strong evidence that such a combined framework is necessary to understand both problems. We are now extending this approach and going toward practical applications. For example, we are involved in a collaboration with Mars on granulation and the fabrication of chocolate.