58th Annual Report on Research 2013 Under Sponsorship of the ACS Petroleum Research Fund

The jamming of materials can be a curse or a blessing - a curse when it prevents food grains from pouring from a hopper; a blessing when it allows a soft, jamming robot to grasp objects or move about.  When a powder, emulsion, or granular system  is subjected to increasing density or pressure, it jams:  abruptly developing a nonzero yield stress, while remaining in a disordered, fluid-like configuration.  Jamming has been recognized as a true phase transition for a number of model systems[1].  

Our research utilizes one of the best-studied models: soft spheres in 2d and 3d, to probe the basic science behind jamming in the presence of additional constraining forces.  These might arise from walls whose confining shapes model realistic porous materials, or apertures whose placement can be varied and widths can be dynamically controlled. Alternatively, constraints might arise from fixed obstacles around which mobile grains will jam as their density is increased.  Obstacles can provide a form of "quenched disorder" which has been suggested to be an additional axis of the jamming phase diagram [2].

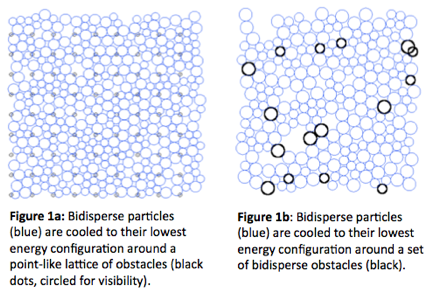
 The most fruitful work in the first year of our ACS PRF grant was jamming in the presence of obstacles.  In collaboration with the Liu group in the Physics Dept. at the University of Pennsylvania, we have run simulations in C++ to probe the effect of both regular and irregular arrays of fixed particles – both point-like (see Figure 1a) and extended (see Figure 1b)  – on the jammed state.

Among our results for soft spheres in 2d are:

i) The bulk modulus of a jammed configuration increases substantially, e.g. by a factor of over a hundreed in an N=256 sphere system as the density of a lattice of obstacles (as in Figure 1a) increases from 0 to 25% .

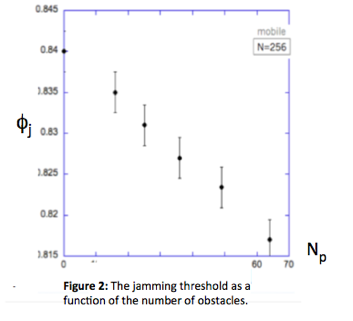
ii) The jamming threshold φ _j decreases linearly over this range of obstacle densities (see Figure 2).

iii) The ability of a lattice to support jamming is dependent on the geometry of the lattice.  In 2d, a hexagonal lattice of the same density will support jamming more effectively (lower threshold) than will a square or random lattice.  

iv) The traditional jamming threshold is a point of discontinuity, at which the number of contacts per mechanically-stable particle rises from 0 to the isostatic value of <z> = 2d – 2d/N.  This rule also seems to hold at sufficiently low obstacle densities.  (Obstacles themselves are exempt from the rule, and tend to be hypostatic.) But at higher obstacle densities, the discontinuous jump in <z> is reduced by virtue of a novel situation: isolated clusters of mechanically-stable particles below jamming.

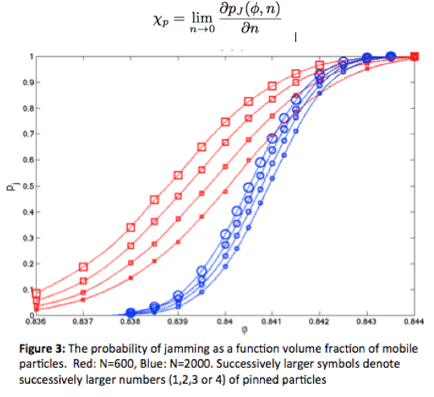
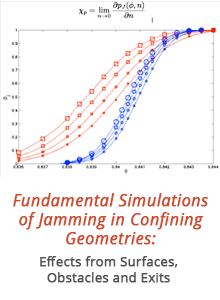
v) Figure 3 shows p_j( φ , N_p),  the likelihood that a system jams at volume fraction φ   parametrized by N_p the number of extended obstacles. The dilute-disorder limit, in which the density, n, of pinned particles approaches zero, allows us to define a new quantity, the "pinning susceptibility":

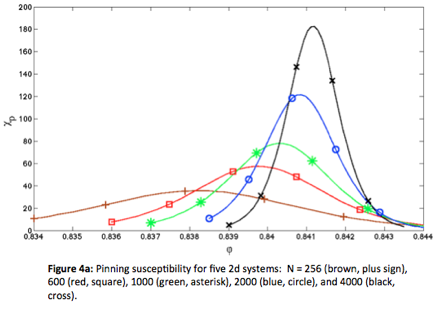
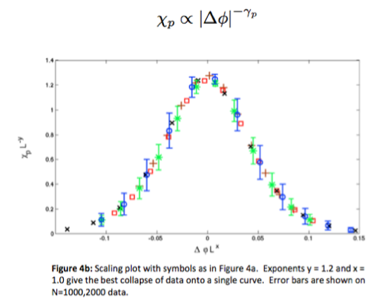
vi) χ _p is postulated to diverge in the thermodynamic limit at the jamming threshold, as the peaks in Figure 4a which grow with N suggest. Figure 4b shows a successful attempt to use a finite-size scaling argument to collapse all of these functions onto a universal curve.  The curve is thought to be independent of interaction potential, in that both harmonic and hertzian interactions yield data that collapse onto the same curve.

vii) The scaling collapse of Figure 4b yields a critical exponent γ _p

In two dimensions, our preliminary results indicate γ _p = 1.2. Questions under current investigation are whether scaling, and the numerical value of this new exponent hold in 3d. We also ask whether the horizontal axis of a scaling plot like Figure 4b is best represented in terms of a length scale like "L",  or (as with other systems above their upper critical dimension) whether there is no diverging length scale and finite-size scaling depends more fundamentally on N.

Other interesting questions, raised by these results from our first year of the grant, are the subjects of future work. Which regular lattice geometry best supports jamming in 3d? Does isostaticity hold at the jamming threshold in the presence of obstacles?  Will isostaticity, the jump in contact number, or some other key feature be altered, when obstacles exceed some critical density of their own?

During the first fiscal year of this grant (January, 2012 - August, 2013) five undergraduates have benefitted from the experience of collaborating in research at Swarthmore College, and also as visitors at U. Penn.  Two have given posters at our annual Sigma Xi sponsored poster session (another will do so early in the second grant year.)  Three undergraduates have been coauthors on talks given at the American Physical Society (APS) meetings in March 2012, 2013.   Four students have now received their BA's;  two of these have gone on to graduate programs in the physical sciences (Cornell University, University of Delaware).   The other two are employed in business and industry, utilizing computational skills acquired during our research.

The ACS PRF grant has helped me, the PI, greatly.  It has both energized my research in a new field, and cemented a valued collaboration with experts at U. Penn.  I have given research talks at U. Penn, once speaking to all undergraduate NSF REU students at the Materials Research Science and Engineering Center (MRSEC) at the Laboratory for Research on the Structure of Matter (LRSM).  I gave a talk for non-specialists to the Swarthmore faculty. In addition to the contributed talks at APS March meetings, I am now able to give invited talks on our research - the first will be at Oberlin College. Finally, this research has given me visibility; e.g. invited to serve on a major NSF MRSEC review team at the University of Chicago.

References:

[1] "The jamming transition and the marginally jammed solid," A. J. Liu and S. R. Nagel, Annual Reviews of Cond. Mat. Phys. 1, 14.1-14.23 (2010).

[2] "Jamming in systems with quenched disorder", C.J. Olson Reichhardt, E. Groopman, Z. Nussinov, and C. Reichhardt,
Phys. Rev. E 86, 061301 (2012).