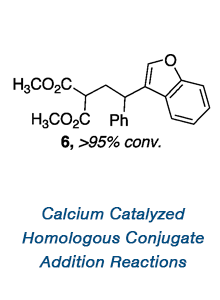
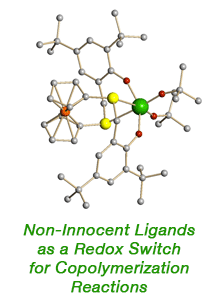
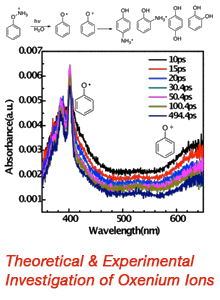
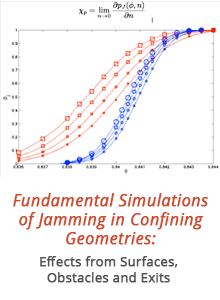
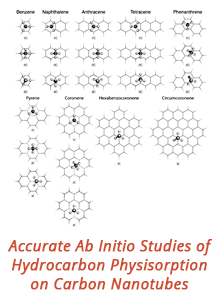
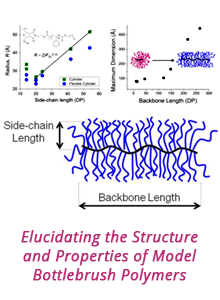
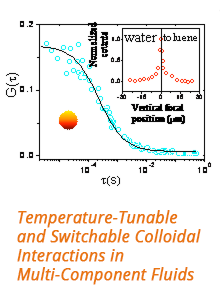
58th Annual Report on Research 2013 Under Sponsorship of the ACS Petroleum Research Fund

Thin solid sheets exhibit a rich variety of patterns under generic confinements and featureless distribution of forces. This morphological diversity reflects the coupling between geometry and mechanics in elastic sheets, a problem whose foundations had been set many years ago. This field has seen recently a surge of research activity, driven by studies that demonstrated its relevance for morphogenetic processes, and by developing material applications at ever decreasing scales that enable the mechanical control of tiny structures. A major theoretical challenge posed by this progress is the development of a formalism that explains the basic mechanisms for pattern formation in thin sheets under various loadings and confinements. The hurdle here is associated with the highly nonlinear nature and the geometric complexity of the problem when the sheet thickness becomes exceedingly small. This complexity requires the development of new concepts and methods, beyond traditional ones, such as “post-buckling” methods. During 2012-2013, the ACS-PRF grant continued to support our theoretical studies in this field. The main effort in this year, carried by the postdoctoral researcher Dr. Evan Hohlfeld, has focused on studies of wrinkle patterns on curved substrates and the mechanisms by which those wrinkles patterns become unstable.

The adhesion of a solid sheet onto a curved substrate underlies numerous biomechanical phenomena and a broad range of technologies, from the production of a hemispherical electronic eye to wear-resisting coating of joint implants. Despite the rich phenomenology and technological importance of this problem, numerous basic questions have not been addressed yet: What are the general conditions under which blisters, wrinkles and crumples emerge? Can these (and possible other) modes of deformation coexist in the same pattern? Can delamination be avoided if the curved substrate is sufficiently soft? Can a crumpled shape appear also on a stiff, spherically shaped substrate?

Similarly to the unavoidable distortion of distances in planar maps of earth, solid sheet must develop elastic stress when attached to a curved substrate. The inevitable stress may relax through several basic types of instabilities: Delamination (blistering) of the sheet from the substrate; formation of defects (particularly if there is some crystalline structure) where the sheet deforms plastically; and wrinkle – that involve a simultaneous deflection of the sheet and the attached substrate. This wrinkling instability is particularly important in cases where the curved substrate is sufficiently soft, such as a liquid drop. Dr. Hohlfeld and I have studied the characteristics of the wrinkle pattern, its dependence on key physical parameters, such as the stiffness of the substrate, its curvature, and the thickness and size of the sheet. Furthermore, by adopting and developing the “far-from-threshold” formalism, introduced in our previous works (ACS-PRF supported), this recent work identified a novel mechanisms by which the wrinkle pattern becomes unstable, giving rise to the formation of crumpled zones, in which the stress is likely to be highly focused.  In addition to this understanding, the work with Dr. Hohlfeld has led to new insights on the mechanisms that govern the characteristic wavelength of wrinkle patterns. In addition to the traditional mechanisms, associated with uniaxial tension or substrate stiffness, our recent work revealed another, purely-geometric mechanism,  in which the wrinkle wavelength is simply the geometric mean of the sheet’s thickness and radius of curvature of the substrate. This discovery has numerous implications on our understanding of wrinkle patterns. Another key result pertains to the strong influence of wrinkling on the suppression of delamination of thin sheets from stiff curved substrates.