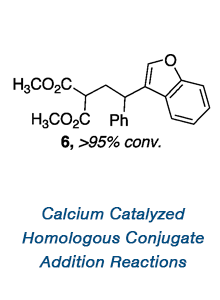
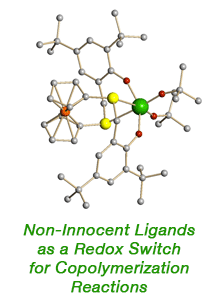
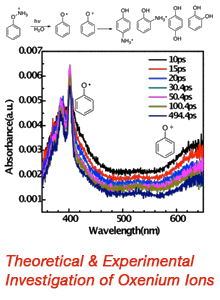
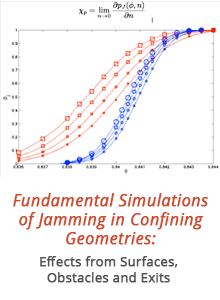
58th Annual Report on Research 2013 Under Sponsorship of the ACS Petroleum Research Fund

The thermodynamics of supercooled water has received quite a bit of attention from the scientific community.  This research group has been among those studying it, and our research has focused on the hypothesis that water has a second critical point, located too deeply in the supercooled region to be accessible to experiment. In the past year, we turned also our attention to the dynamics of supercooled water, in particular the thermal conductivity.  The thermal conductivity of water is known to decrease with decreasing temperature, a behavior that is highly anomalous.  Simulations by Kumar and Stanley in 2011 found a minimum in the thermal conductivity of the TIP5P model of water.  This minimum occurred deeply in the supercooled region.  Because thermal conductivity is known to diverge near the liquid-vapor critical point of a pure fluids—this is an effect of critical fluctuations—we sought to investigate the possibility that the increase in thermal conductivity in deeply supercooled simulation models of water might also be an effect associated with the hypothesized second critical point.  When we applied the mode-coupling theory of critical phenomena to this hypothesized critical point, we found that any fluctuation effect would be far too small to be observable.  However, we have proposed a simpler explanation, associated with the thermodynamics of water.  It has been noted that in the cold-stable and supercooled regions, the thermodynamics of water closely follows Bridgman’s formula, in which thermal conductivity is proportional to the speed of sound.  One consequence of the hypothesized second critical point would be a line of minima of the speed of sound lying close to the Widom line, or line of maximum fluctuations of the order parameter.  Therefore the minimum in the thermal conductivity, if indeed it exists in real water, may also be explained in terms of thermodynamics: it may be associated with a minimum in the speed of sound.  We published this research in a paper in Physical Review E.  John Biddle presented a poster on this research at the annual March Meeting of the American Physical Society, and gave talks on it at the CEAFM-Burgers-GWU Research Symposium on Environmental and Applied Fluid Dynamics (Baltimore, Maryland), Graduate Research Interaction Day at the University of Maryland at College Park (College Park, Maryland), and the International Conference for the Properties of Water and Steam (London, England).  In addition, we are now working in collaboration with Fernando Bresme at Imperial College (London, England) who carries out simulations.  We hope that this collaboration will cast further light on the relationship of dynamics to thermodynamics in supercooled water.  This collaboration is underway but still in an early stage.

            We are also investigating the thermodynamic behavior of supercooled aqueous solutions in light of the second-critical-point hypothesis.  In particular we have examined experimental data for aqueous solutions of glycerol and NaCl, intending to extend our group’s equation of state for supercooled water, which includes a liquid-liquid phase transition and a liquid-liquid critical point, to solutions.  This equation of state was published in 2012 by V. Holten and M. A. Anisimov.  Archer and Carter, of the National Institute for Science and Technology, have published data showing that the increase in the isobaric heat capacity upon supercooling moves to lower temperatures and is suppressed in magnitude as NaCl is added.  At mole fraction 0.1, no increase is observed.  We find this to be in agreement with a well-developed body of theoretical work on mixtures.  When response functions such as isobaric heat capacity and isothermal compressibility are measured at constant concentration (as they nearly always are in practice) rather than at constant chemical potential, the near-critical behavior of these response functions changes: response functions that had diverged strongly in the pure fluid diverge only weakly, and those that had diverged weakly remain finite.  An equation of state based on this body of theory gives an excellent quantitative match to Archer and Carter’s Data.  A graph showing this behavior is the Table of Contents image for this report.  We are also in the process of examining data on aqueous solutions of glycerol and extending the two-state model to that system.  In a similar fashion as for NaCl, we will present an extension of Holten and Anisimov’s equation of state to this system.  Additionally, a previous shows a phase transition in deeply supercooled aqueous solutions of glycerol.  There exist thermodynamic data on supercooled water-glycerol systems, and Murata and Tanaka have observed a phase transition in supercooled aqueous solutions of glycerol.  The transition that they report is from one homogeneous phase to another; however, we propose that for experiments at constant concentration, there must also exist a two-phase region. We will offer an estimate of the size and position of this region in terms of temperature, pressure, and concentration of solute. Within a month we intend to submit a manuscript that will include this research to the Journal of Physical Chemistry B.

            One student, John Biddle, was supported by the PRF grant for the academic year 2012-2013 and the summer of 2013.  He received his Master of Science degree in physics from the University of Maryland, College Park in May 2013 and advanced to candidacy as a Ph. D. student in physics in May 2013.  The research described above will be part of his Ph. D. dissertation.