58th Annual Report on Research 2013 Under Sponsorship of the ACS Petroleum Research Fund

Summary and impact

Using a new four roll mill (FRM) device, we have performed exploratory studies of wormlike micelles (WLMs) with two representative behaviors: shear thinning and shear banding. In both cases, the fluid “resists” a transition from extensional to shearing flow. For shear thinning fluids, shear rheology tends to dominate the flow, resulting in significant gradients in deformation rate near the boundaries. For shear banding fluids, this gradient occupies an unobservably small region, with concomitant non-monotonic behavior in both the local deformation rate and flow type, which we believe is related to the extensional rheology of the fluid. Our results hold impact for both processes and formulations involving WLMs. When dealing with highly shear thinning or shear banding fluids, one should anticipate that geometries producing mixed flows with significant extensional components will have shear that is highly localized near the boundaries, with the remainder of the flow being dominated by extension.

This research has built new experimental tools in the PI's lab (including FRM and velocimetry) that complement previous expertise with WLMs. Our work has also benefited from collaboration with Gary Leal, whose expertise in modeling polymeric fluids has enabled predictions of WLM flows which can be compared with our experimental results, providing important physical insight into how underlying fluid behavior influences the observed flows. As a result, the PI and collaborators have become, to our knowledge, the only group in the world currently performing detailed studies of viscoelastic micellar fluids in controlled mixtures of shear and extensional flow.

Detailed progress

We have assembled and validated a temperature-controlled FRM device for video microscopy measurements (Figure 1). The flow is characterized by a nominal deformation rate, G₀, and applied flow type parameter, Λ₀, equal to the ratio of rotation rates of rollers 2 and 4 relative to 1 and 3 (Λ₀=1 for 2D extensional flow, 0 for shear flow).^1,2 Tracer particles are introduced into the fluid, the flow is illuminated from the sides, and a digital video camera takes images of the flow field at up to 60 Hz. Images can either be used to produce time-lapse photographs (Figure 1, right, greyscale) or analyzed using standard PTV algorithms to quantify the velocity field (red arrows).

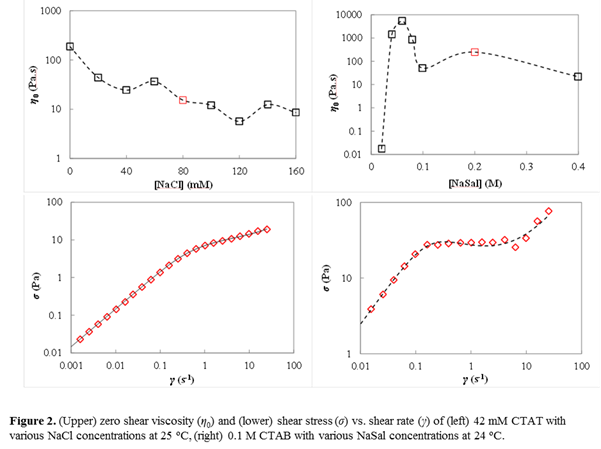
Corn syrup, WLMs comprised 42 mM hexadecyltrimethylammonium p-toluenesulfonate (CTAT), 80 mM sodium chloride (NaCl) and 0.1 M cetyltrimethylammonium bromide (CTAB), and WLMs comprised of 200 mM sodium salicylate (NaSal) were used as representative examples of Newtonian, shear-thinning, and shear-banding fluids, respectively. Linear viscoelastic (LVE) and flow curve measurements of the non-Newtonian samples were fitted with the one-mode Giesekus model (Figure 2).³

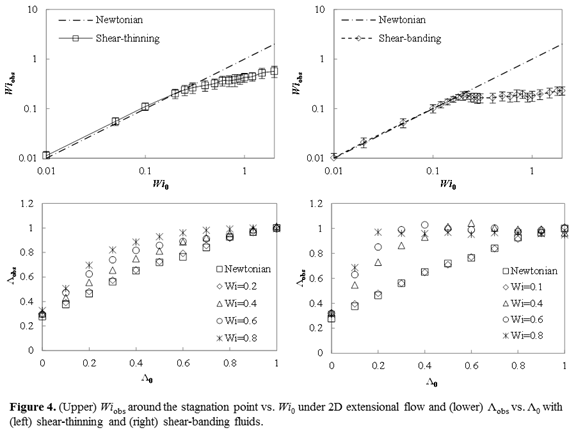
In the FRM, linear dependence of the measured deformation rate near the stagnation point, G_obs, on the roller speed was obtained for the Newtonian fluid for all L₀, validating the device design (Figure 4). For WLMs, the deformation rate is characterized by the dimensionless Weissenberg number, Wi=Gτ, where τ is the characteristic relaxation time from LVE measurements. Time lapse images from the samples at various Wi show interesting behavior (Figure 3). Whereas both Newtonian and shear thinning samples exhibit similar qualitative behavior (top), the shear banding sample deviates significantly. At Wi<0.2 (middle), the sample behaves similar to a Newtonian fluid. However, for Wi>0.2 and L₀>0, the observed flow appears similar to 2D extensional flow (L₀), despite rollers rolling at different speeds.

Figure 4 shows the observed Wi near the stagnation point, Wi_obs=G_obsτ, versus the nominal applied Wi, Wi₀=G₀τ, for the WLMs (the flow type parameters, Λ₀ and Λ_obs, are defined in a similar manner). The Newtonian result, Wi₀=Wi_obs, is shown for comparison. For both fluids, Newtonian behavior was observed for Wi₀<0.2. For the shear thinning sample, Wi_obs deviates below Wi₀ for Wi₀>0.2, with a non-zero slope. By contrast, for the shear-banding fluid, Wi_obs first shows a maximum near Wi₀=0.2, followed by a plateau of Wi_obs~0.18 until a slight increase for Wi₀>1. Based on previously published simulations in the FRM, this non-monotonic behavior could be associated with extensional thickening of the fluid.

We also studied the behavior of the fluids in mixed flows (0<Λ₀<1). For the Newtonian fluid, Λ_obs>Λ₀ for Λ₀<1 (Figure 4), indicative of non-idealities in the FRM due to unavoidable contributions from the outside walls. Quantitatively similar behavior was observed with both WLM samples for Wi₀<0.2. For both fluids, when Wi₀>0.2, Λ_obs is higher than that observed in the Newtonian case. For the shear thinning fluid, this deviation becomes continuously more severe as Wi₀ is increased. For the shear banding fluid, a plateau of Λ_obs ~ 1 is obtained for all Wi₀>0.2. The lower bound of this plateau in L₀ decreases as Wi₀ increases. This result implies that for the shear banding fluid, the flow segregates into regions of shear (or weak deviations thereon) and pure extension when a significant extensional component of the flow exists and Wi₀>0.2.

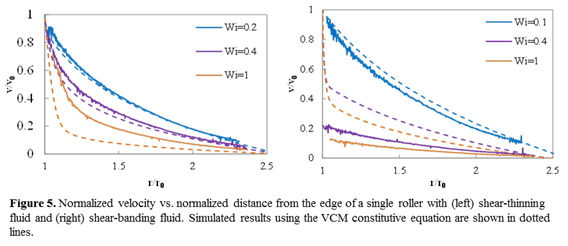
To further probe this behavior, we analyzed the velocity field near individual rollers (Figure 5). Absent a full 2D model, the flow field around the moving roller can be approximated by 1D shear flow between two concentric cylinders. For the shear thinning fluid with Wi₀>0.2, significant yet smooth gradients in local shear rate were found close to the rollers. This is typical of a shear thinning fluid in a geometry with a stress gradient, which explains why Wi_obs<Wi₀ for Wi₀>0.2. Predictions of the velocity profile using the VCM model previously developed for WLMs^4,5 is in qualitative agreement, although the model significantly overpredicts the shear rate gradient.

For the shear-banding fluid at Wi₀=0.1, the velocity profile is similar to that obtained with a Newtonian fluid (Figure 5). For Wi₀>0.2, however, we surprisingly find that the dimensional velocity profile (not shown) was quantitatively identical regardless of Wi₀, and coincides with the plateau of Wi_obs under 2D extensional flow (Figure 4). The VCM model predicts qualitatively similar behavior. This is in contrast to thin gap flow between concentric cylinders.⁵ We thus hypothesize that, for sufficiently curved geometries (or those with significant stress gradients), shear banding is highly localized near the no-slip surface.