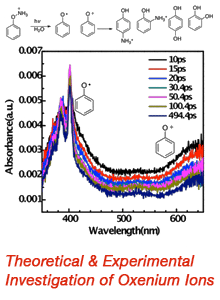
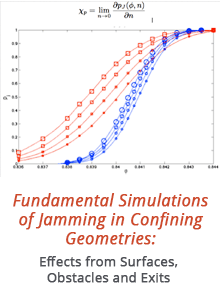
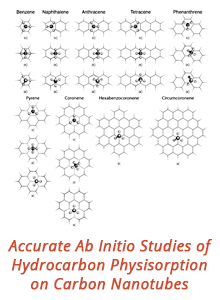
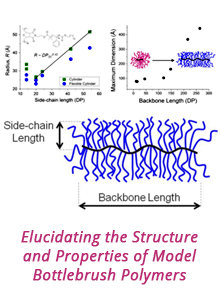
58th Annual Report on Research 2013 Under Sponsorship of the ACS Petroleum Research Fund

Predictive modeling and high-fidelity simulations are now widely recognized to play an important role in advancing the fundamental understanding of turbulent reacting flows. One of the major challenges in analysis of such flows is associated with the physics of turbulence. It is commonly acknowledged that the optimal means of capturing the detailed, unsteady physics of turbulent reacting flows is via large eddy simulation (LES) with inclusion of accurate subgrid scale (SGS) models. The filtered-density function (FDF) methodology has proven particularly effective for this closure. The effectiveness of the FDF is due to its inherent capability to account for the chemical reaction effects in an exact manner. However, consideration of complex chemistry along with the FDF is still a challenge due to high computational costs. Therefore, the central part of this research has involved utilizing efficient methods to handle complex chemical kinetics in FDF simulations. This research also aims to provide insight into cause of irreversibilities in turbulent reacting flows. This is essential to improve the efficiency of turbulent combustion systems. Significant progress has been made in this period to achieve these objectives. This has enabled application of the FDF to investigate more complex turbulent flames. Educational efforts associated with this research include training two Ph.D. students who will continue contributing to the field beyond the duration of this grant. A summary of the progress made during this period is provided below.

1) Efficient implementation of detailed chemical kinetics:

Efficient methods are developed and implemented for accurate, affordable simulation of turbulent reacting flows using LES/FDF with complex chemical kinetics. Our efforts in this period was focused on implementation of the Rate-Controlled Constrained-Equilibrium (RCCE) method. In RCCE, a reduced number of scalar equations are considered to govern the evolution of (slowly varying) constraints on chemical reaction. Implementation of the RCCE within the FDF is conducted by considering a set of differential equations for the constraints. The unconstrained (rapidly varying) species are assumed to be temporarily in equilibrium; their compositions are determined by maximizing the entropy subject to the instantaneous values of constraints. In this period, the RCCE formulation is assessed for efficient implementation within the FDF framework. The effectiveness of the RCCE and the significant savings it provides are demonstrated in stirred reactor simulations. These reactors consist of particles, identical to those in the Monte Carlo (MC) solution of the FDF. Figure 1 shows some of the results for methane oxidation kinetics involving 12 constraints (29 chemical species) and 133 reaction steps. The RCCE predictions are performed and validated using direction integration of the same kinetics. As shown in Fig. 1(a), the RCCE provides accurate prediction of ignition delay in a perfectly stirred reactor with various initial conditions. The RCCE is also able to represent the effect of mixing on reaction. This is illustrated in partially stirred reactor predictions (Fig. 1(b)). The RCCE results compare very well with those of direct integration.

2) Improvement of the FDF/RCCE solver on massively parallel platforms:

The objective of this task is to develop improved methodologies for efficient implementation of the FDF/RCCE on massively parallel platforms. The FDF/RCCE solver involves large number of MC particles. With the large number of particles, due to intensity of RCCE computations, the solver requires enormous computation times. To handle such intensive simulations, scalable parallelization at the MC particle level and balanced load among CPUs are essential. These problems are effectively addressed in this project by using a hybrid domain-decomposition/particle-partitioning parallelism strategy. In this approach, the computational domain is decomposed into sub-domains with (approximately) the same number of particles. In each sub-domain, particles are randomly and equally partitioned, and assigned to a pool of processors. The hybrid method has been implemented on distributed memory as well as shared-memory multi-processor architectures.

3) Development of the entropy FDF for irreversibility analysis of turbulent reacting flows:

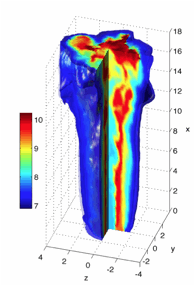
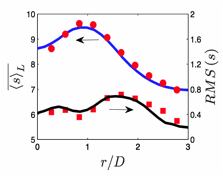
Analysis of irreversibilities (entropy generation) is an effective approach to improve the second-law efficiency of turbulent combustion. Alongside our chemical kinetics implementations, a new methodology is being developed that facilitates such analysis by including the transport of entropy within the FDF framework. The filtered entropy is considered in LES, which includes several unclosed source terms contributing to entropy generation and hence, second-law efficiency losses in combustion. These terms describe the entropy production due to viscous dissipation, heat conduction, mass diffusion and chemical reaction. All the unclosed terms in the filtered entropy transport equation are provided by the entropy FDF. An exact equation is developed for the FDF which is modeled by a set of stochastic differential equations (SDEs). The system of SDEs include a stochastic process for entropy and is solved by a Lagrangian MC procedure. The entropy FDF is applied to a turbulent nonpremixed methane jet flame (Sandia Flame D) and the results are validated against experimental data. Our work in this period has involved validation of the entropy FDF. Figure 2 shows the instantaneous filtered entropy field  resulted from formation of large-scale coherent structures. The predictive capability of the entropy FDF is shown by comparing the entropy statistics derived from the Sandia thermo-chemical data. Figure 3 show the good agreements of the mean filtered and RMS values of entropy with the data.

Figure 1. The RCCE (blue solid lines) compared with direct integration (red dashed lines) for methane oxidation kinetics. (a) Ignition delay in perfectly stirred reactor. (b) Reaction along with mixing in a partially stirred reactor.

Figure 2. Instantaneous contours of entropy (kJ.kg.K) predicted by the entropy FDF in Sandia Flame D simulations.

Figure 3. Radial variation of entropy (kJ.kg.K) statistics: (a) mean filtered entropy, (b) RMS of entropy predicted by the entropy FDF in Sandia Flame D simulations. Solid lines denote the FDF predictions; symbols denote the experimental data.