58th Annual Report on Research 2013 Under Sponsorship of the ACS Petroleum Research Fund

Our current research has been to design algorithms to calculate relaxation selective pulses (AIM IIB).  We have also continued to characterize the diffusion and aggregation processes (AIM IIA) for a "simple" dye, sunset yellow.

Design of Relaxation Selective Pulses (AIM IIB):

Research Goal:  In porous media, the relaxation times, T2 (transverse) and longitudinal (T1), are inversely proportional to pore size. The goal of AIM IIB was to design radiofrequency (RF) pulses that are able to selectively null the magnetization for a particular choice of relaxation parameters and/or values of the diffusion coefficient. Such pulses could be used for studying diffusion between different pore sizes using a variety of 3D NMR experiments (e.g., diffusion/diffusion, relaxation/relaxation, and diffusion/relaxation correlation experiments).

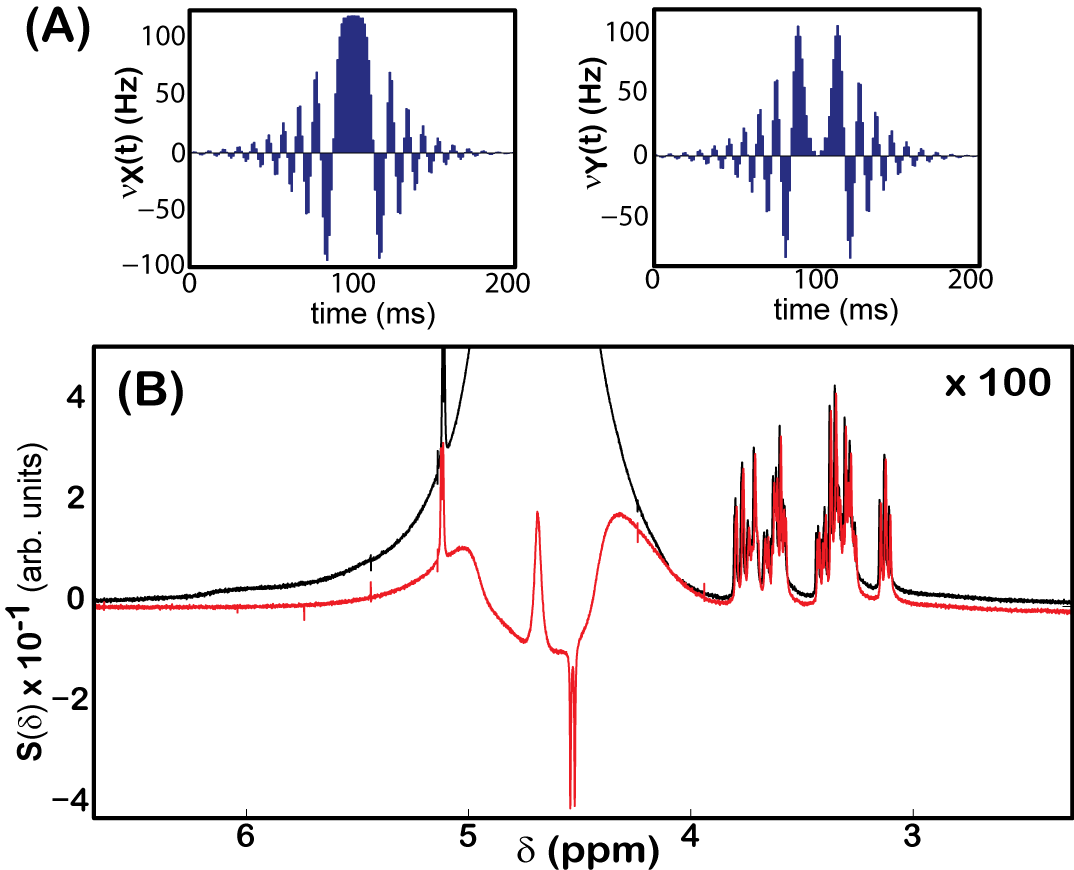
Progress to date: Our group has developed pulses that selectively zero the magnetization based upon the T₂ relaxation parameter of the spin [T₂ is the time constant for decay of the transverse magnetization, and T₁ is the time constant for the magnetization to reach its equilibrium value about the applied magnetic field]. To develop these pulses, the PI's group modified the gradient-descent pulse engineering (GRAPE) algorithm developed by the Khaneja group in order to search for pulses that were robust to pulse imperfections, e.g., offsets, field inhomogeneities, and T1 relaxation. These algorithms were adapted in order to enable us to numerically search for relaxation selective pulses. The convergence of the GRAPE algorithm and the “discovery” of optimal pulses were found to be very sensitive to the initial input pulse. However, the algorithm was found to converge quickly when adiabatic pulses were used as initial input.  Furthermore, modifications to the algorithm to ensure smooth pulse shapes were applied, which will be critical when optimizing pulsed field gradient shapes.   An example of an optimal pulse that we developed is shown in Fig. 1(A); which zeros magnetization with T₂=22.68 ms and T₁= 539 ms.  The total pulse length was 203.4 ms, which was must faster than the time needed (379.2 ms) to suppress the solvent magnetization based upon an inversion recovery sequence.   The pulse in Fig. 1(A) was used to suppress the water resonance in a 0.05 M glucose solution doped with [Mn⁺²] = 4 X 10^-4 M.   A doublet from the anomeric proton in b-D glucose is clearly seen after water suppression in Fig. 1(B).    We have also derived a connection between spin relaxation and nonlinear spin dynamics under an effective radiation damping field, which should help in choosing better trial functions for the GRAPE optimization.  This work has been submitted for publication.

Future Directions:   Since a smoothing constraint was added into our optimal control algorithm, we are now optimizing combined RF pulses with shaped pulsed field gradients in order to selectively zero the magnetization based upon the diffusion coefficient.  We are also trying to improve the sensitivity of diffusion measurements twofold by optimizing square wave inversion pulses combined with pulsed field gradients. 

Figure 1.  Solvent suppression in a 0.05 M solution of glucose in a 1:9 v/v H₂O/D₂O doped with [Mn⁺²] = 4x10^-4 M.  (A) Optimized relaxation selective pulses that suppress the water resonance with T₂=22.63 ms and T₁=539 ms.  (B) Spectra (red) after application of the relaxation selective pulses in (A).  A 95.4% reduction in the water signal relative to the 90-acquire spectrum (black) was found.  An inverted doublet from the anomeric ¹H in b-D glucose was clearly resolved.

Using RF pulses to constrain spectral distribution functions in porous media (AIM IIA):

Research Goal: The relaxation and diffusion distribution and joint distribution functions can provide valuable information about the chemical composition of oil, and also the porosity and pore size distribution. Information about these distribution functions can be inferred from a variety of NMR experiments. The goal of AIM IIA was to determine a set of optimal pulse sequences that could be used to constrain the relaxation and diffusion distribution functions.

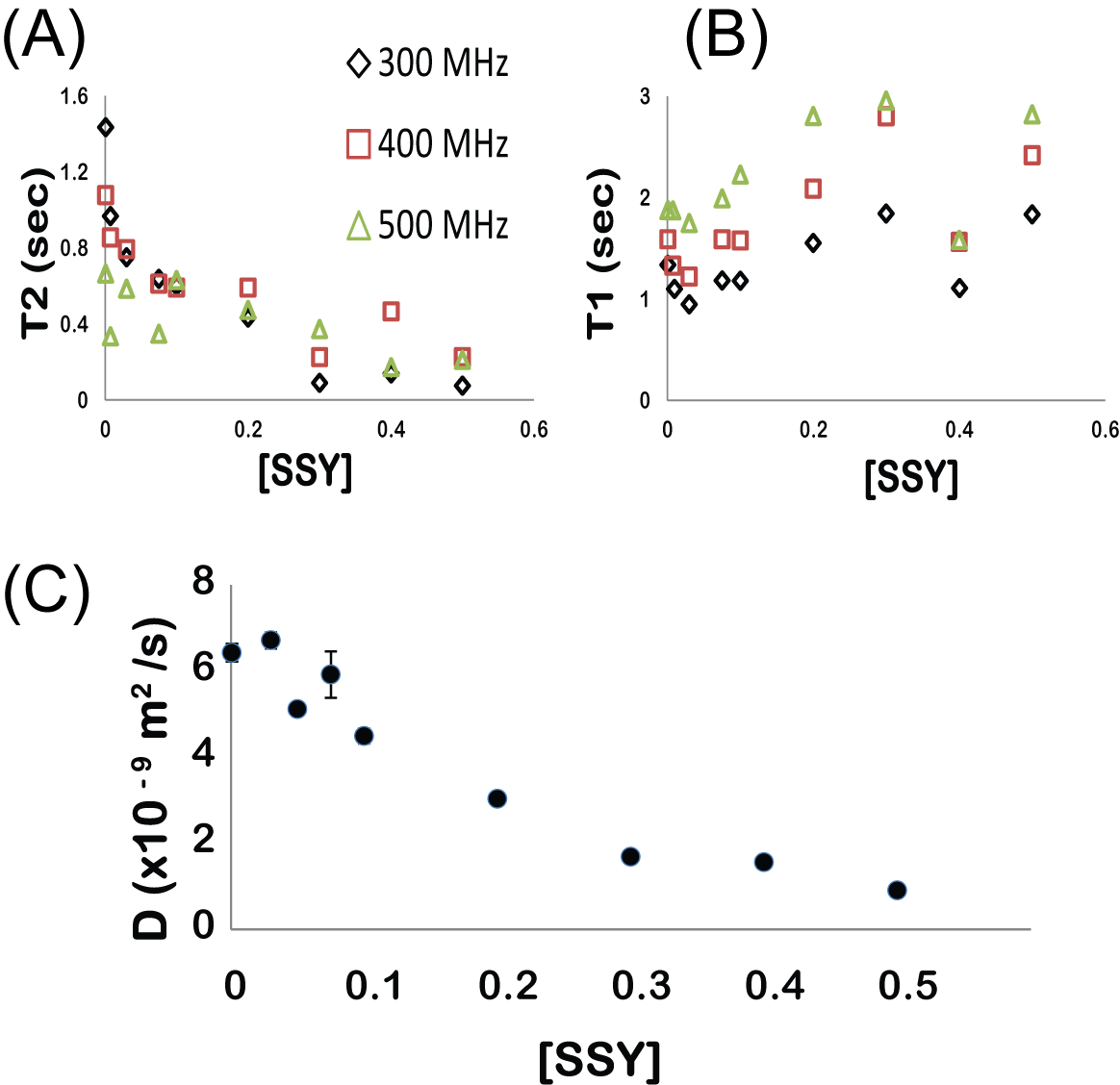
Progress to date:   We have studied the aggregation in sunset yellow (SSY), a chromoionic dye, by measuring the diffusion coefficient vs. [SSY] in both D₂O and in DMSO using ¹H NMR and UV-Vis spectroscopy and by measuring the effects of salt concentration and cationic valency on aggregation.   The observed diffusion coefficient, measured using a pulsed field gradient stimulated echo sequence, is shown to decrease with increasing [SSY] in Figure 2(C).  We have also studied the relaxation properties, T₁ and T₂ and NOE factors, vs. [SSY] and field strength (300 MHz, 400 MHz, and 500 MHz).   Figure 2(A) and 2(B) plots the measured transverse (T2) and longitudinal (T1) relaxation times vs. [SSY] at 300 (black diamonds), 400 (red square), and 500 MHz (green triangle) fields.

Part of the goal of our research is to design NMR experiments to test and constrain different models of aggregation in organic dyes.  While there are a variety of theoretical models that have been proposed to describe the aggregation process in organic dyes such as the monomer-dimer, isodesmic, modified isodesmic, and the Israelachvili models, there does not appear to be a model that fits the aggregation process over a wide range of dye concentrations.  Some of our theoretical work has demonstrated that the isodesmic and Israelachvili models are equivalent and connected to aggregation described by the reversible Smoluschowski equations.  While most of the theoretical models assume that the maximum cluster size can be arbitrarily large, we are investigating the effect of enforcing a finite maximum aggregate size on the predicted aggregate distributions. 

Future Directions:  With these measurements, we are in the process of extracting important dynamical information, such as rotational correlation times.   We are also developing theoretical models for the relaxation and diffusion parameters vs. aggregate size in SSY in order to derive aggregate distributions that are consistent with the experimentally observed data.

Figure 2.  Measured (A) T2 and (B) T1 relaxation times vs. [SSY] at 300 (black diamond), 400 (red square), and 500 MHz (green triangle) fields.  The uncertainties in relaxation times were less than 16 ms.  (C) The self-diffusion coefficient measured using a pulsed field gradient stimulated echo experiment vs. [SSY].