Reports: ND752426-ND7: Thermodynamics of Nanoconfined Equilibrium Polymerizations
printer friendly
The objectives of the
proposed investigation center around the hypothesis that nanoconfinement
will influence the thermodynamics of equilibrium polymerizations. The entropy of confined chains decreases
on confinement, and in the case of strong confinement, confinement entropy
scales with molecular size to a power greater than 1.0. The mean field result[1]
yields a scaling of the confinement entropy with N2 and Monte Carlo
simulations[2]
give a scaling with N9/4, whereas for theta-solvents, the scaling
goes as N to the third power.2,[3] The latter
scaling with N3 is also consistent with experiments for
poly(ethylene glycol) in nanochannels created by alpha-toxin.[4] Thus, in the strong confinement
regime, the change in Gibbs free energy on propagation (DGp = DHp - TDSp, where DHpis the enthalpy change on
propagation and DSp is the entropy change) might be expected to be
modified by confinement. In turn,
the equilibrium constant Kp will decrease
from the bulk value (for reactions having negative enthalpy and entropy changes
on propagation) by an amount that depends on chain length raised to some power
and nanoconfinement size raised to a negative
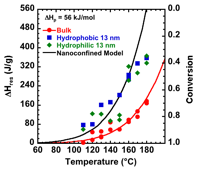
power. Our first test of this hypothesis have focused on making measurements for methyl methacrylate polymerization under nanoconfinement. Bulk poly(methyl methacrylate) has a ceiling temperature of approximately 220 °C. Under nanoconfinement in 13 nm pores of controlled pore glass (CPG), we find that the ceiling temperature shifts to lower temperatures, as shown in the Figure, where the residual heat of reaction is plotted on the y1 axis and the conversion is plotted on the y2 axis. The shift in the ceiling temperature to lower temperatures is consistent with a decrease in the entropy of propagation under nanoconfinement. The fit to the nanoconfined data in the Figure assumes that to a first approximation, this in entropy change does not vary with temperature. Work in the coming year will focus on modeling the results to determine the scaling involved, as well as performing similar experiments for other equilibrium polymerizations.
[1]. C. Y. Kong and M. Muthukumar, "Polymer translocation through a nanopore. II. Excluded volume effect," J. Chemical Physics, 120, 3460 - 3466 (2004).
[2]. T. Ishinabe, "Conformational Properties of a Polymer Chain Confined between Two Plates," Journal of Chemical Physics, 83 (1), 423 - 427 (1985).
[3]. A. Cacciuto and E. Luijten, "Self-Avoiding Flexible Polymers under Spherical Confinement," Nano Letters, 6 (5), 901 - 905 (2006).
[4]. S. M. Bezrukov, I. Vodyanoy, R. A. Brutyan, and J. J. Kasianowicz, "Dynamics and Free Energy of Polymers Partitioning into a Nanoscale Pore," Macromolecules, 29, 8517 - 8522 (1996).
