58th Annual Report on Research 2013 Under Sponsorship of the ACS Petroleum Research Fund

The primary accomplishment in the past year was adapting a Weibullian "weakest link" statistical theory to explain our experimental results. A collaboration was initiated with Steve Teitel at the University of Rochester to expand our computational abilities. During my sabbatical year (2013-2014), I will focus almost exclusively on implementing a fully parallelized code for three-dimensional, frictional particles.

Weibullian "weakest link" statistics
In our experiments, a cylindrical pile of U-shaped staples is subjected to a linear extentional stress. We detect when the applied force drops, indicating pile elongation, and the statistics of these events analyzed. Previously, our most intriguing finding was that longer piles are significantly weaker than short piles (as described in our 2012 report). This can now be explained through a Weibullian weakest link theory as follows.

The theory assumes that long samples are comprised of N smaller units, each with a length δL, and the sample fails (breaks) if any one of the sub-units fails. The theory further assumes that the probability of failure is proportional to the length δL and scales with the applied force F as a power law with exponent m. The total probability S that a sample of total length L does not fail is the product of N individual probabilities for success: S=∏[1-F^mδL]. Taking the logarithm of each side and keeping terms to highest order results in the approximation that S ≈ exp[-LF^m] and that the two-dimensional probability distribution of failure as a function of both applied force F and sample length L is P_f (F,L) = 1 - exp[-LF^m].

If the pile length is held constant, the theory predicts a failure probability that goes as 1-exp[-F^m]. A plot of experimental data at fixed L is shown in Figure 1; the solid line is the best fit of the form 1-exp[-F^m] with m=1. The implication of m=1 is that the probability of a fundamental length sub-unit scales linearly with the applied force.

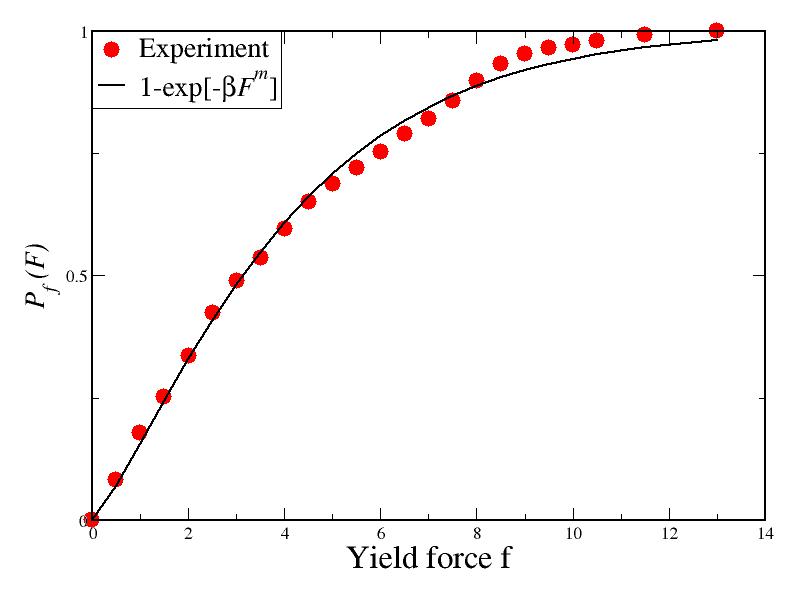
Figure 1: Probability distribution P_f of failure events as a function of applied force f. There is good agreement between experimental data (red dots) and theoretical prediction (solid line) with a single fit parameter, the scaling exponent m. The theory therefore implies that failure of the fundamental length "units" in these systems scales linearly with force.

With the scaling exponent from the fixed-length measurements, we may now make two predictions to further test the theory's applicability. The first is the mean yield force as a function of sample length. This is obtained by integrating the two-dimensional probability distribution over all lengths: <F_Y>=∫ LF exp[-LF] dF ∼ L^-1. As seen in Fig. 2, the prediction of mean force agrees quite well with the experimentally observed data.

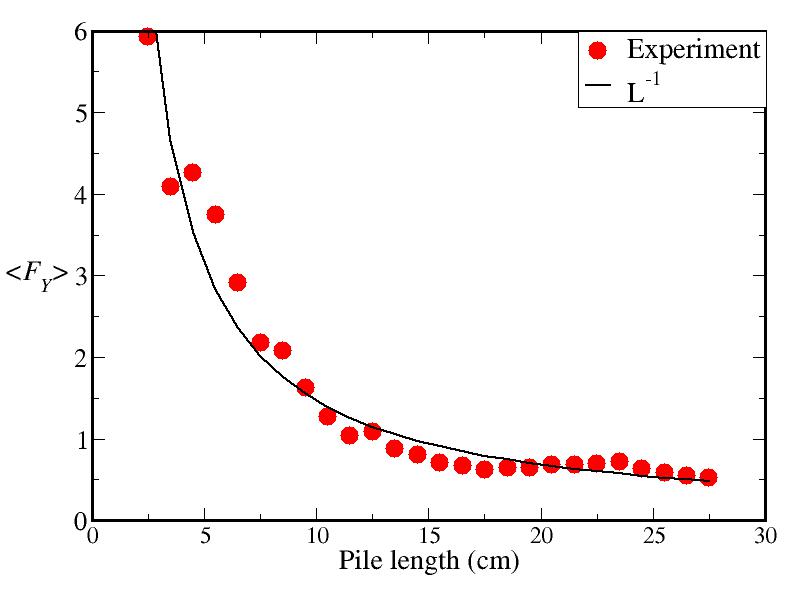
Figure 2: Comparison of experiment and theory for mean yield force as a function of sample length. Theory predicts a simple inverse decay, the exponent having been derived from measurements on yielding at a single length. The fit is the first confirmation that weakest-link statistics apply to elongation of cohesive granular materials.

We emphasize again that a measurement taken at a single length has now been used to predict mean failure probabilities at multiple lengths.

Finally, the entire corpus of data, consisting of over 7500 individual slip events, may be collapsed onto a single master curve. The functional form of the master curve is a bit unwieldy, involving the normalized 2-d probability distribution function, but in simplest form it predicts that L^-1log[1-P_f(F,L)/P_f(L)] ∝ F. This is shown in Figure 3; within the standard-deviation error bars, the fit is excellent. The collapse of all the data onto this master curve confirms the applicability of the Weibullian weakest-link theory.

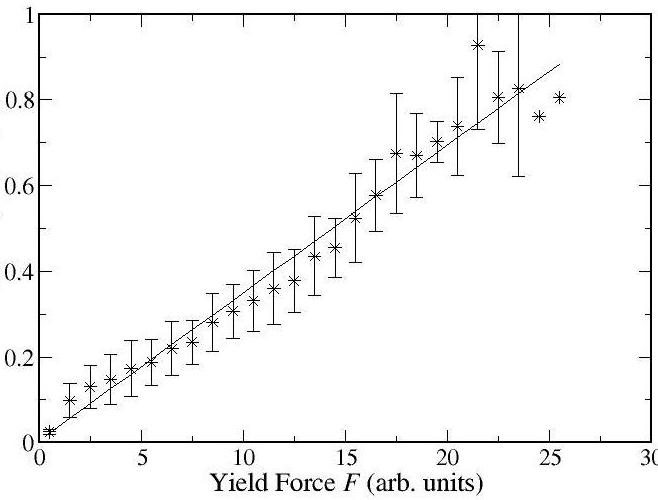
Figure 3: Collapse of the 2-d failure probability distribution function (over 7500 independent yield events) onto a single master curve as predicted by Weibullian weakest-link theory.

Subsequent work will disentangle the statistics of events that occur before and after the single largest rearrangement, testing the assumption that all events may be treated as independent. The Weibullian theory also makes predictions about how yield forces should scale with changes in cross-sectional area and also in response to bending forces.

Computational work
A collaboration with Steve Teitel at the University of Rochester was initiated. Steve's previous work has involved simulations of 2-d round, frictionless particles under shear. We have developed code, parallelized to run on a GPU, for 2-d U-shaped particles under shear and are investigating the shear modulus and response of the pile to various imposed strain-rates.

For my upcoming sabbatical year, I will be working at the University of Rochester to extend these simulations to 3-d samples in both shear and extensional geometries.