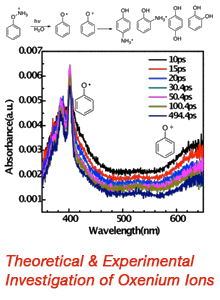
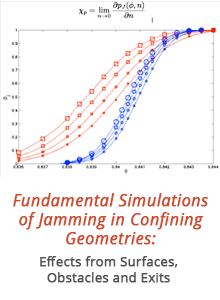
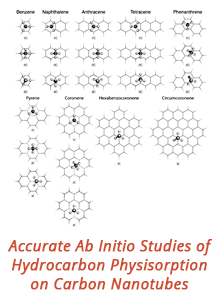
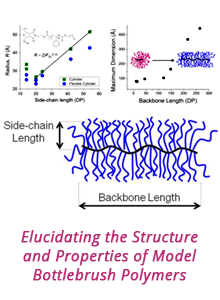
58th Annual Report on Research 2013 Under Sponsorship of the ACS Petroleum Research Fund

Asphaltenes are operationally defined as the heavy, aromatic fraction of crude oil that is soluble in toluene, but insoluble in n-heptane.   Aggregation of asphaltene molecules significantly impedes petrochemical extraction, processing, and transport.  However, the molecular mechanism of asphaltene self-assembly remains unclear.   In recent years, several studies have employed atomically detailed simulation models to investigate asphaltene self-assembly.  The computational expense of atomistic models, though, severely limits the scope of such simulation studies.  In particular, such models cannot easily address the length-scales, time-scales, and concentrations that are relevant for asphaltene self-assembly in complex petrochemical mixtures.  Accordingly, we have proposed to develop much more efficient, low-resolution "coarse-grained" (CG) models for performing extensive, systematic simulation studies of asphaltene aggregation on realistic scales for a wide range of conditions and mixtures.  During the first period of this grant, we have developed the computational methodology that is necessary for parameterizing and simulating such models, as well as parameterized accurate and efficient solvent models for simulations of asphaltene self-assembly that are planned for the coming year. 

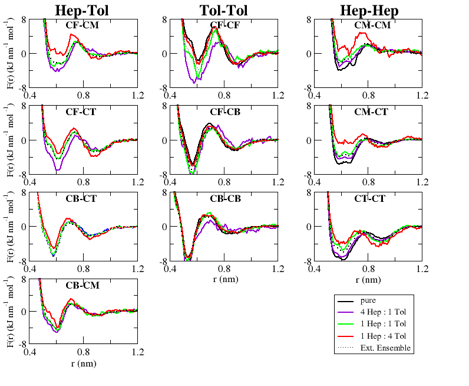
As a first necessary objective towards this goal, we have developed bottom-up CG solvent models to accurately reproduce the structure of heptane/toluene mixtures.   We first performed simulations with the atomically detailed OPLS model to sample configurations from the canonical ensembles for a range of mixtures.  We represented each molecule with three sites in order to reproduce their shape and flexibility.  After mapping each ensemble to this representation, we applied the multiscale coarse-graining (MS-CG)/generalized-Yvon-Born-Green (g-YBG) method within an extended ensemble framework to determine the single set of transferable interaction potentials that provide a variationally optimal approximation to the many-body potential of mean force (PMF) for each mixture.  The following figure presents the CG pair force functions that are optimized for each individual mixture, as obtained from MS-CG/g-YBG calculations for each system, as well as the extended ensemble potentials, which are optimized for transferability.  Although the development of transferable interaction potentials remains an outstanding challenge, the CG models developed from the extended ensemble framework should accurately model the solution structure for each heptane/toluene mixture.

Realistic simulations of asphaltene aggregation should be performed in the constant pressure ensemble, both in order to treat volume fluctuations during self-assembly and also to address various petrochemical conditions.  However, the vast majority of bottom-up methods for parameterizing accurate CG models have been designed for simulating systems at constant volume.  Constant pressure simulations are typically performed by introducing empirical ad hoc corrections to the intermolecular potentials.  These modifications artificially alter the intermolecular interactions and do not guarantee correct volume fluctuations.  Accordingly, our second objective has been to implement the pressure-matching algorithm proposed by Das and Andersen (DA) for rigorously sampling the constant NPT ensemble in simulations of CG models.  In essence, this algorithm parameterizes an effective renormalization of the virial equation to account for the atomic degrees of freedom that have been eliminated from the CG model.  We have implemented the DA method into our framework for obtaining effective CG interaction potentials.  We have also introduced the renormalized virial equation as a modified barostat within the LAMMPS software package.  As a first validation of these developments, we have numerically demonstrated that the calculated pressure correction vanishes in the case that no coarse-graining is performed.  This test demonstrated the sensitivity of the calculated pressure correction to both the basis set and also the long-range cut-off used for the intermolecular potential.  This test calculation also provided insight into correlations between volume fluctuations and errors in the CG pressure. 

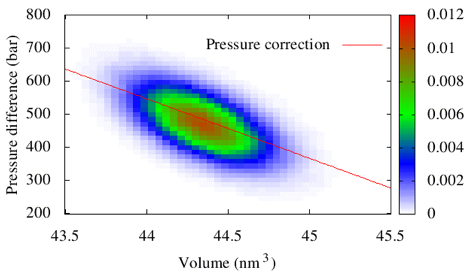
As a second validation, we have reproduced the model calculations reported by DA.  In this model calculation, DA determined the pressure correction that is necessary to reproduce the pressure of a system of Lennard-Jones (LJ) particles, when half of the LJ particles have been eliminated from the CG model.  The figure below presents an intensity plot for the two-dimensional distribution describing the correlation between the error in the CG pressure (when using the standard virial equation) and the sampled volume.  The solid line presents the calculated pressure correction for the renormalized virial.  This correction agrees with the correction calculated by DA to within 3% error in the first order and within 15% error in the second order.  Given the uncertainty in our knowledge of some aspects of the DA calculation and the sensitivity of the pressure to the CG potential, these discrepancies appear entirely reasonable. 

We are currently applying this methodology for our heptane/toluene models and, ultimately for our model asphaltene systems.  Importantly, this not only paves the way for constant pressure simulations of CG models for asphaltenes, but will also provide the first demonstration of this rigorous pressure correction for complex molecular systems. 

Finally, we have also been preparing top-down CG models that have historically provided a more accurate treatment of thermodynamic properties. Simulations with our initial models generated too large a surface tension.  Consequently, we have been fine-tuning the parameters of the top-down toluene model via the multi-property fitting method of Klein and coworkers.  Our model is now quite close to being able to reproduce the correct interfacial tension.