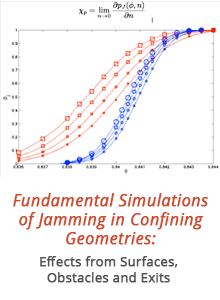
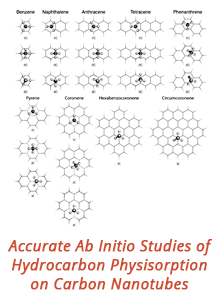
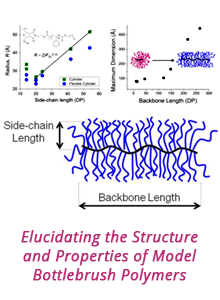
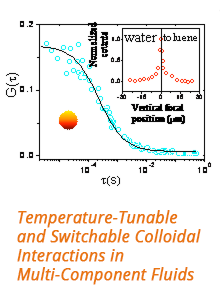
58th Annual Report on Research 2013 Under Sponsorship of the ACS Petroleum Research Fund

Drop coalescence plays a central role in a number of industrial and natural processes involving emulsions of small drops of one fluid in a second fluid.  Coalescence is of common occurrence in applications as diverse as crude oil production, foodstuffs (e.g. shelf-life of mayonnaise), sprays, and solvent extraction.  Coalescence is also important in the production of advanced materials (e.g. sintering), growth of raindrops, and life sciences (e.g. membrane fusion).  In many processes in the petrochemical industries, it is necessary to remove a dispersed water phase from a continuous oil phase.  In the petroleum industry, water-in-oil emulsions are formed during the production of crude oil.  If the oil is not dehydrated (demulsified), the presence of water in the oil can result in corrosion of pipes, deactivation of catalysts, and increased costs in transporting the unwanted water.  As surface-active species are present in many applications, the goal of this research is to advance the fundamental understanding of coalescence of surfactant-laden drops.  When two drops are slowly brought together and first touch, a small liquid neck forms between them.  The expansion of the neck is controlled by the Laplace pressure which diverges when the curvature of the interface is infinite at the point where the drops first touch.  The major objective of the research is to probe by simulation and experiment the nature of the singularity in the dynamics when the drops are covered with a monolayer of an insoluble surfactant.

In the research, the system being considered is isothermal and consists of two identical spherical drops of radii A of an incompressible Newtonian fluid of constant density d and constant viscosity m that are surrounded by a dynamically passive gas that exerts a constant pressure on the drops.  The surface tension of the clean liquid-gas interface is T.  Moreover, both drops are taken to be covered uniformly with a monolayer of an insoluble surfactant.  In the simulations, the drops will be brought together quasi-statically and a small neck will be formed between them.  A definition sketch is provided in the graphic image that can be found in the Table of Contents.  In the first year of the project, our goal has been to analyze by simulation the flows and the topological changes in the interface shapes that ensue to probe the dynamics in the vicinity of the singularity and to uncover the various regimes of coalescence.

The flow and surfactant transport problems are governed by the continuity and the fully nonlinear Navier-Stokes equations for the velocity and the pressure, and the nonlinear surface convection-diffusion equation for surfactant concentration.  The effect of surfactant concentration on surface tension is governed by a nonlinear equation of state.  These equations are solved subject to the traction and kinematic boundary conditions along the free surfaces and symmetry boundary conditions along the axis of symmetry.  The initial condition is such that the fluid within the just joined drops is quiescent and the concentration of surfactant is uniform along the liquid-gas interface.

During this first year, we have developed the computational algorithm and computer code to solve the free boundary problem comprised of the aforementioned equations.  Our approach is a method of lines algorithm that utilizes an implicit, adaptive finite difference time integrator and a Galerkin/finite element method for spatial discretization.  To deal with the free and deforming boundary of the flow domain, the domain is discretized with an adaptive elliptic mesh generation algorithm.

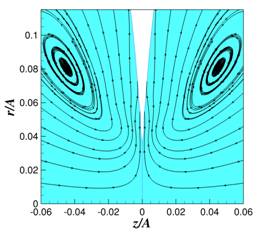
Once the code was developed, it was benchmarked against another code that had been written by a more senior graduate student whose research is focused on coalescence in the absence of surfactants.  All of the tests carried out to date have shown that the new code predicts results that are identical to the other, older code.  In the figure that is attached to this progress report, we present an instantaneous streamline plot depicting the flows within two coalescing drops at the instant in time when the minimum radius of the connecting bridge equals 0.04A for the situation in which the Ohnesorge number Oh = 0.6 (the Ohnesorge number equals the viscosity m divided by the square root of the product of density d, radius A, and surface tension T).

After extensive validation tests, we have turned our attention to studying coalescence in the presence of surfactants.  Among other things, we have been exploring the effect of surfactant concentration on the scaling law(s) for the dependence on time t of the radius r(t) of the small bridge that connects the two drops.  Aside from identifying different regimes of coalescence and uncovering scaling laws governing the variation of bridge radius with time, another goal of the research is to develop similarity solutions that characterize the interface shapes in the different scaling regimes.

The present ACS/PRF grant already has had a tremendous positive effect on the PI's career and the graduate students involved in the project.  Upon receiving the grant, the PI was able to recruit one of the top students in the first year class of graduate students who had just started their graduate students in the School of Chemical Engineering at Purdue University.  The PI now has two graduate students working on coalescence, one who is being supported by the ACS/PRF grant and another by unrestricted funds available to him.  Thanks to the ACS/PRF grant, the PI is well on his way to building a strong program to study diverse problems of basic and applied importance in the coalescence field.  Also thanks to the ACS/PRF grant, the new student was able to rapidly learn the required techniques to successfully tackle the research problem at hand while being mentored by the more senior student who is focused on coalescence in the absence of surfactants.