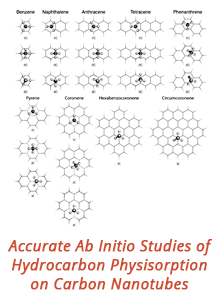
58th Annual Report on Research 2013 Under Sponsorship of the ACS Petroleum Research Fund

We have constructed an apparatus that subjects small (3-5 ml) samples of complex fluids to vertical vibrations at a controlled frequency and acceleration.  The fluids we have been testing are 1) concentrated suspensions of non-Brownian, spherical glass beads in aqueous solution, and aqueous solutions of neutralized Carbopol gel.  The latter is a transparent solution of polymer macromolecules that are charged at pH values close to neutral; the repulsive interaction caused by the charges causes a liquid-to-gel transition when a base is added to Carbopol solutions.  Since many fluids used in oil recovery contain particulates and exhibit a yield stress, and are exposed to vibration from drilling processes, this research is directly relevant to the petroleum industry.

Both fluids show complicated and interesting behavior when subjected to controlled vibration.  Depending on the conditions, the suspensions of glass spheres exhibit “crowns,” in the form of periodic indentations near the edge, and which may or may not be accompanied by “craters,” or holes that permeate the suspension to the supporting plate.  At stronger conditions, the suspension samples form a mound or miniature “volcano” like structures;  ultimately, it is even possible to cause a lump of highly concentrated suspension to rise up into a single sphere that floats over the vibrating plane. 

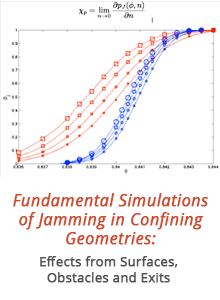
By collecting these observations at varying conditions, we have formed a phase diagram that represents results at different accelerations, frequencies, density differences and sphere diameters.  Because the transitions disappear when the suspensions are closely density-matched, a scaling argument was developed based on the idea that the plate acceleration drives a fluid-to-solid “jamming” transition.  Jamming occurs as the particles accumulate on the supporting plate as it accelerates upward.  Those arguments yield a dimensionless group that describes the time scale for the particles to jam relative to the period of the vibration.  The interesting behavior we see occurs when this group varies from 1 to 10, with the most important transitions, such as the formation of “volcanoes” or “floating spheres,”  occurring when it is greater than 5. 

To further test the hypothesis that it is an acceleration-dependent, fluid-to-solid transition that underlies the phenomena we observe, we have been performing simulations with OpenFOAM, an open-source toolbox for computational fluid dynamics.  The simulations make use of the finite-volume numerical method, with the volume-of-flow (VOF) approach to modeling the air-suspension interface.  We have modified the code that comes with the OpenFOAM software to include an acceleration-dependent viscosity that gets large when the acceleration is directed opposite to gravity.  The results support the hypothesis that an acceleration-dependence is the principal cause of the behavior we see.

As mentioned above, in addition to suspensions of glass spheres in aqueous solution, we have been working with particle-free solutions of Carbopol polymer.  Carbopol is a polymerized form of polyacrylic acid that forms “microsponges” with diameters of 5-6 microns, surrounded by a layer of hydrophilic polymer strands.  These entities swell or shrink depending on the pH of the solution, forming a jammed or gelled medium that does not flow at rest. 

The behavior of these gels when subjected to vibration differs significantly from the suspensions we are studying, but the underlying physics may be linked.  An example of our observations is shown in the Table of Contents (TOC).  Under select conditions, vibration of gelled Carbopol solutions yields a sample with holes arranged in a regular order.  We have seen as few as 2 holes, and in some cases more than 8.  In the TOC, there are 7 holes at the vertices of a pentagon, outside of which a new layer of holes has partially formed.  Although they are not hard spheres as in the suspensions, the microsponges in Carbopol constitute a dense core of soft particles that are crosslinked enough so as to preclude overlap.  Furthermore, it is known that the heterogeneity in a Carbopol gel extends over length scales that can be significantly larger than the microsponge diameters.  This heterogeneous microstructure is a feature that these gels share with particulate suspensions.

To provide additional insight into the topological changes we observe, we are using classical lubrication theory for shallow liquid layers.  Lubrication theory has been used successfully to describe the wave patterns (i.e., Faraday waves) that develop in vibrated, shallow layers of Newtonian liquids.  There are also reports in the literature of adapting it for a stick-slip transition that can lead to the growth of protuberances and holes in vibrated non-Newtonian fluids.  In our modification, we use this theory to examine the possible consequences when the acceleration varies sinusoidally, and the viscosity also varies in time.  The linearized form of lubrication theory predicts surface shapes that agree qualitatively with our results.  In particular, an integer number of periodically arranged indentations is predicted.