58th Annual Report on Research 2013 Under Sponsorship of the ACS Petroleum Research Fund

This PRF project focuses on elucidating the interactions, phase behavior, and aggregation dynamics of polymer-grafted shaped nanoparticles (pgsNPs) in simple solvents and in polymer melts. We have made significant progress towards this goal in this first year of funding, and our accomplishments include: (1) development of a quantitative image analysis software to characterize experimentally observed aggregation of pgsNPs within polymer films as a function of time, and (2) elucidation of the aggregation mechanism and growth kinetics of pgsNPs via coarse-grained models and simulations. This research has been presented at three conferences and two manuscripts are currently being prepared for publication based on these results. The PRF award has provided funds to support a postdoctoral researcher and allowed the involvement of three other students (1 graduate and 2 undergraduate). The award also contributed towards the PI's recent promotion to associate professor.

Quantitative Image Analysis

To investigate the growth kinetics and morphology of pgsNP aggregates, we have developed software in Matlab that analyzes SEM images of NP aggregates obtained by our experimental collaborators. The software inputs a set of raw SEM images of the NP-laden polymer thin film taken at intermittent time points following the deposition of NPs into the polymer film. The software then utilizes various algorithms to process these raw images and identify individual NPs and their clusters in each processed image (Fig. 1). The software then computes and outputs a number of structural characteristics of the NP clusters, including their size, radius of gyration, shape anisotropy ratio, aspect ratio, asphericity, fractal dimension, number of branches, and backbone length. The software also gathers statistics for each property as a function of time.

Figure 1: Overall scheme for automated image analysis (top panel). The raw SEM images are first pre-processed to determine their size and scale and to improve their contrast and remove noise. The images are then converted into binary image using a thresholding algorithm. The binary images are then subjected to a number of morphological (erosion and dilation) and segmentation procedures to yield the final processed image that allows identification of individual NPs and NP aggregates. These processed images allow determination of properties of NP aggregates, such as their fractal dimension (bottom left). The software also allows us to gather statistics, such as the aggregated size distribution (bottom right).

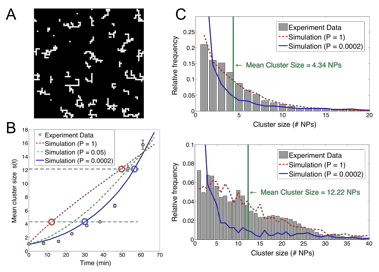
We have used the software to investigate the growth kinetics, fractal dimension, and size distribution of poly(vinylpyrrolidone)-grafted Silver nanocube aggregates in a polystyrene thin film. Our calculations reveal exponential growth with respect to time (Fig. 2B). The observed kinetics also applies to other NP shapes, including Silver nanoprisms, Silver nanospheres, and Gold nanorods. We have also computed the fractal dimension D_F of the NP aggregates from correlations in their spatial density. The computed D_F is ~1.4, confirming the formation of fairly linear NP aggregates. While the mechanism behind the formation of linear structures is not fully understood, it likely arises due to preferential growth of NP clusters through their ends. One hypothesis is that the aggregation of NPs pushes the intervening polymer grafts out of the nanojunction, inhibiting the assembly of other NPs at the nanojunction and instead promoting their assembly through the NP chain ends. We are currently testing this hypothesis using computational models described in the next section. We have also investigated the distribution of aggregate sizes: at early times the distributions exhibit a non-monotonic, power-law decay with increasing aggregate size while at later times the distributions exhibit a peak at intermediate sizes (Fig. 2C).

Figure 2: (A) Lattice Monte Carlo simulation model of NP aggregation (NPs shown as white squares). (B) Comparison of experimental NP cluster growth rates against Monte Carlo simulations conducted at different sticking probabilities P. (C) Size distribution of NP aggregates from experiments (gray bars) at early (top panel) and late stages (bottom panel) of aggregation, compared with distributions obtained from simulations at two different values of P (dotted red lines: diffusion limited; solid blue lines: reaction-limited)

Computational Modeling of NP Aggregation

We developed two types of computational models to elucidate the mechanism by which the pgsNPs aggregate. First, we used kinetic lattice Monte Carlo simulations (Fig. 2A) to investigate if the NPs aggregate through a diffusion- or a reaction-limited mechanism. The simulations were started from a disordered configuration of NPs at experimental coverage densities. The diffusion of NPs, and of their aggregates, was treated as a random walk on a square lattice with Stokes-Einstein diffusivities. Whenever NPs, or their clusters, collided with each other, they stuck irreversibly with a fixed probability P to form larger clusters; P = 1 represents a diffusion-limited scenario while P << 1 represents a reaction-limited scenario. The simulations were then used to predict NP aggregation growth rates, aggregate size distributions, and aggregate morphologies. By comparing the simulations with experiments, it was found that the experimental growth rates were more consistent with a reaction-limited mechanism, while the aggregate size distributions and morphologies seemed more consistent with a diffusion-limited aggregation (Fig. 2B,C). We are currently exploring several hypotheses (long-range hydrodynamic interactions between aggregates; preferential aggregation through ends; and time-dependent diffusion rates) to explain this surprising result.

Second, we are employing coarse-grained models of polymer-grafted Silver nanocubes and Monte Carlo simulations previously developed in our group to investigate the "pathway" of NP assembly. Specifically, we aim to elucidate the minimum free-energy path in the configurational space (i.e., the orientation of the two nanocubes) that two nanocubes adopt as they approach each other from a distance and lock into their eventual lowest-free energy configuration. Our preliminary calculations suggest that the face-to-face nanojunction forming nanocubes first approach each other in an edge-to-edge configuration but then "slide", and not "rotate", into their final face-to-face configuration. We are currently extending this approach to other NP shapes and also computing three-body interactions between pgsNPs to explain their aggregation into near-linear structures.