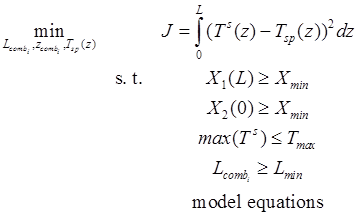58th Annual Report on Research 2013 Under Sponsorship of the ACS Petroleum Research Fund

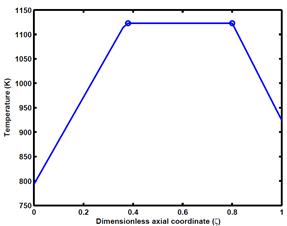
In the first year of the grant, we have focused on identifying new means for manipulating the spatial temperature distribution and achieving thermally balanced configurations in authothermal microchannel reactors. In these systems, a set of endothermic reactions is carried out concurrently with one or more exothermic reactions, with the latter supplying heat to the former. The reactions occur in millimeter high channels separated by thin, catalyst coated plates. Ideally, all the heat generated at every axial position is consumed by the endothermic reactions. However, in practice, the rates of the exothermic and endothermic reactions can be vastly different; the rates of heat generation and consumption at different longitudinal locations in the corresponding channels are equally mismatched. Synchronizing the rates of heat generation and consumption remains an open problem. Solutions such as creating longitudinal gradients in the activity of the catalyst in one or both of the channels, or implementing several longitudinally-distributed feed points for the inlet stream to the exothermic channels (Figure 1, top), have proven to be difficult to implement in practice.

A new approach was investigated, namely, using a segmented catalyst geometry (Figure 1, bottom) comprising alternating catalytic and inactive (blank) sections in the exothermic channels, to impose an optimal longitudinal temperature profile in autothermal microchannel reactors.

Figure 1: Distributed feed and proposed segmented catalyst configurations for combustion channel.

The problem of identifying the optimal number, length and longitudinal position of the catalytic and blank segments was solved using a novel, two-tier optimization formulation, consisting of simultaneously determining the optimal temperature profile and the catalyst geometry that results in the heat generation rate distribution that establishes this profile. Specifically, out a model-based optimization problem was formulated, seeking to solve:

where i, L_combi and z_combi represent, respectively, the number, length and axial position of the catalytic segments in the exothermic channels, T_sp(z) is the value of the optimal wall target temperature at z, T^s(z) is the temperature of the wall plate at z. The constraints impose, respectively, lower bounds on the conversion in the exothermic and endothermic channels, a maximum on the possible temperature of the wall plates, a minimum length for each catalyst segment and, finally, ensure that the equations of the mathematical model of the reactor are satisfied.

A decomposition algorithm was proposed to solve this large-scale, mixed-integer, infinite-dimensional problem:

1)      Render the problem finite-dimensional by parameterizing the target temperature profile T_sp(z) We relied on a piecewise linear representation as shown in Figure 3.

Figure 2: Temperature profile parameterization.

2)      Fix the value of the integer decision i to 2 (i.e., assume the optimal configuration comprises two catalytic segments), and solve the resulting nonlinear optimization problem using the algorithm previously introduced in (Zanfir et al., AIChE J., 2011, 57, 2518–2528).

3)      Increase the value of i by one, and re-solve the optimization problem.

4)      Compare the value of the objective function at 3) with the objective at i-1. If the difference is below a pre-defined threshold, stop. Otherwise, return to 3) and repeat the process.

To validate the theoretical concepts, a prototype autothermal system for carrying out the (endothermic) methane steam reforming reactions, supported by the (exothermic) catalytic combustion of methane was considered. These systems hold high promise in the processing of methane and carrying out gas-to-liquids conversion on a small scale.

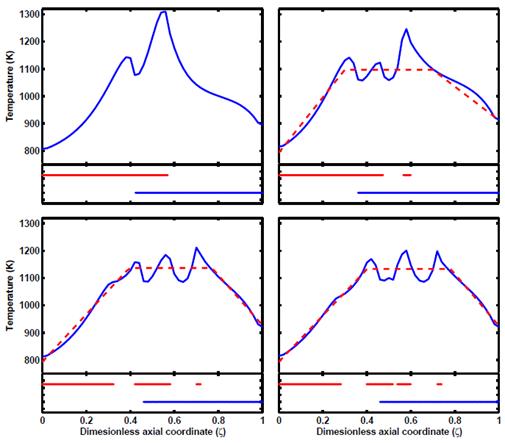
The system was described using a detailed two-dimensional (2D) reactive flow model comprising a catalytic wall plate and the adjacent exothermic and endothermic half-channels. The optimization calculations resulted in a four-segment catalyst configuration for the combustion channels (Figure 3). The length of the catalytic zones increases almost exponentially from the inlet of the channel to the exit. This is an intuitive result, given the need to modulate the heat generated by combustion, whose reaction rate is much larger than the rates of the reforming reactions. The optimized reactor is superior to the base (non-segmented) case, having a much lower maximum operating temperature at the same conversion.

Subsequently, it was shown that segmenting the reforming catalyst (along with the combustion catalyst) does not improve the temperature distribution in the reactor and leads to a deterioration in performance (lower reforming conversion) due a reduction in the catalytic surface area available for the reforming reactions.

Figure 3: Target (dashed) and actual optimal (solid) temperature profiles for the base case (top left), two- (top right), three- (bottom left), and four-segment (bottom right) configurations. Optimal catalyst configuration shown under each plot (combustion catalyst shown above reforming catalyst configuration; the inlet of the combustion channel is on the right-hand side) (Pattison et al., I&ECR, in press).

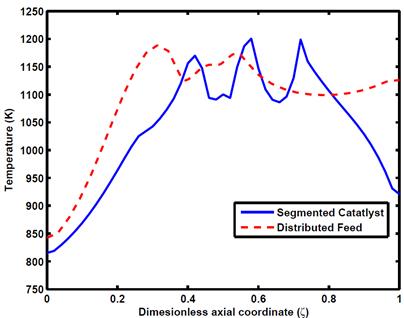
Further, a comparison was made betweenthe optimal design with a hypothetical distributed-feed reactor. The optimal location of four fuel feed points was computed using a modified version of the algorithm above. The resulting temperature profiles are presented in Figure 4, demonstrating that the proposed segmented geometry successfully emulates a distributed-feed configuration.

Figure 4: Comparison of reactor temperatures in a distributed feed reactor (dashed) and the optimal segmented catalyst reactor with four catalyst segments (solid).

Our work has resulted in two publications (one in an ACS journal) and two conference presentations. ACS funding has been essential in supporting the formation of one graduate student (Richard C. Pattison), enabling him to present his work at a major conference; a senior undergraduate student (Forrest E. Estep) has also been engaged in the project, obtaining invaluable research experience for his graduate studies. The financial support provided by this grant has been essential to the PI, allowing him to build his newly formed research group and to establish new, fundamental modeling and optimization concepts that will be used in the development of new control approaches for microchannel reactors in the second year of the grant. Furthermore, these results are generic and can readily be applied to other systems of practical interest. The grant has also fostered useful interactions with industry, and the aforementioned results have been presented as part of seminars that the PI gave at the R&D centers of several major petrochemical companies.