58th Annual Report on Research 2013 Under Sponsorship of the ACS Petroleum Research Fund

Our study in Year 1 focused on the derivation of analytical solutions for unidirectional flows with first-order Maxwell slip boundary condition, lattice-Boltzmann bounce-back scheme to recover the Maxwell boundary condition, and two-dimensional and three-dimensional slip flows through periodic arrays of cylinders and spheres.

In the slip flow regime, the no-slip boundary condition on solid surface is replaced by the first-order slip condition

,

where u_s is the slip velocity in the direction tangent to the surface, n is the surface normal, and λ is the slip length, which for gas flow becomes a function of the tangential momentum accommodation σ and the mean free path λ_MFP

,

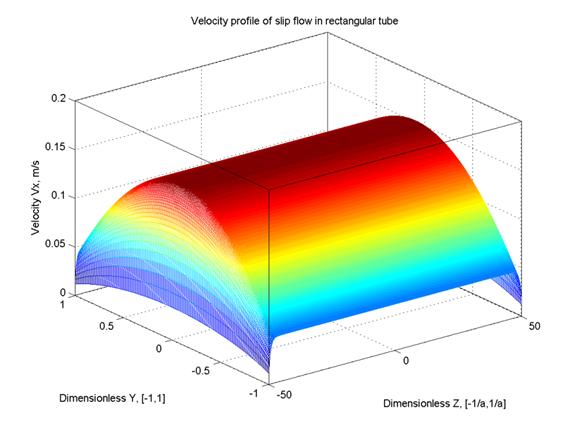
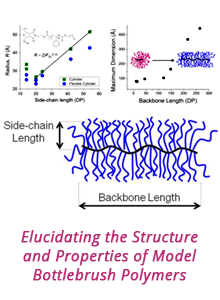
known as the Maxwell slip model. The gas flow in the bulk is still governed by the Navier-Stokes equation. Unidirectional flows when subjected to the Maxwell slip condition still have analytical solutions. Figure 1 shows the profile of a unidirectional flow in a microfluidic channel with rectangular cross-section. The analytical solution was derived using the method of separation of variables.

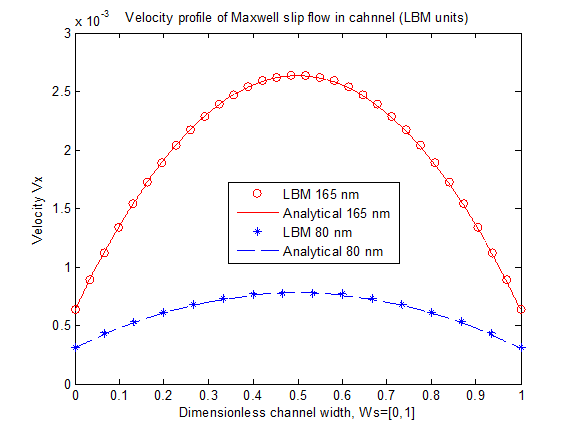
We successfully extended the bounce-back scheme, developed by Yin et al. (2005) for free-slip boundaries at gas-liquid interfaces, to boundaries with Maxwell slip. Numerical solutions of unidirectional flow were in excellent agreement with the analytical solutions.

We then developed two-dimensional and three-dimensional lattice-Boltzmann programs capable of simulating slip flows in arbitrary porous media geometries. Our initial tests focused on two-dimensional flows through square array of cylinders, and three-dimensional flows through periodic array of spheres. Solutions for slip flows through square arrays of cylinders have been presented in several studies (e.g. Chai et al. 2011). There are also many classical results (e.g. Chun and Koch, 2005) for three-dimensional slip flows around an isolated sphere. These two situations thus offer further opportunities for code verification. Our two-dimensional simulations of slip flow through square arrays of cylinders showed excellent agreement with previous studies (Chai et al. 2011). For three-dimensional slip flow through periodic arrays of spheres, when the particle fraction is low, the numerical result should approach those for isolated particles. When the particle volume fraction increases, the slip effect should also become a function of the particle volume fraction Φ. This dependence, which is of importance to the study of suspension of aerosols, has not been previously studied. If particles in the periodic array are allowed to overlap, they will form simple analogs of porous media. For this case, the ratio between the apparent permeability and the Darcy permeability is of significant interest.

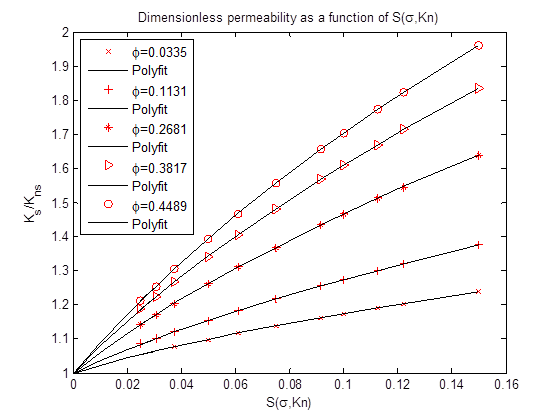
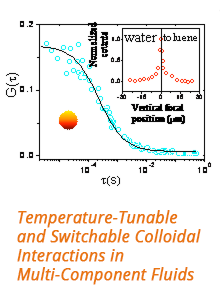
Currently, we have obtained, for simple cubic arrays, the relation between the permeability ratio k_s/k_nsand the dimensionless slip length λ/d for volume fractions 0.034 to 0.449 (Figure 3). We will continue to simulate slip flows in other periodic arrays, namely the face-centered cubic and the body-centered cubic arrays, to establish correlations for the drag force on non-overlapping spheres. Then, we will conduct simulations on arrays of overlapping spheres to establish correlations for the apparent permeability and the Klinkenberg coefficient.

This grant is being used to fully support a PhD student (Lei Wang). The data obtained have been used to support one of the PI's graduate courses (PEGN 601: Applied Mathematics for Fluid Flow through Porous Media). With the support of the grant, the PI developed important computational capabilities in the field of micro- and nanoflows, and built a foundation for future experimental studies that will be conducted using artificial nanopores or rock cores. The PI now has several concurrent projects on fluid flow in unconventional oil and gas rocks funded by industry consortia. Clearly the outcome of this study has generated significant interest from our industry partners.

References

Yin XL, Koch DL, Verberg R, Lattice-Boltzmann method for simulating spherical bubbles with no tangential stress boundary conditions, Phys. Rev. E 73:026301, 2006.

Chai ZH, Lu JH, Shi BC, Guo ZL, Gas slippage effect on the permeability of circular cylinders in a square array, Int. J. Heat Mass Transfer 54:3009-3014, 2011.

Chun J, Koch DL, A direct simulation Monte Carlo method for rarefied gas flow in the limit of small Mach number, Phys. Fluids 17:107107, 2005.

Figures

Figure 1: Analytical slip flow profile in a channel of rectangular cross-section. Dimension in y: 1 unit = 50 nm; dimension in z: 50 unit = 2500 nm; pressure gradient in the x direction: 10⁹ Pa/m; gas (methane) viscosity: µ = 1.1 × 10^-5kg/m-s; gas mean free path: 10.7 nm (25°C, 5 atm); tangential accommodation coefficient: σ = 0.9.  

Figure 2: Comparison between lattice Boltzmann simulations (symbols) and analytical solutions for slip flow (lines). The results were obtained for a 80-nm wide channel and a 165-nm wide channel.

Figure 3: Permeability ratio k_s (with slip) over k_ns (with no-slip) for simple cubic arrays of spherical particles as a function of dimensionless slip s = λ/d. The five sets of data correspond to five different particle volume fractions.