58th Annual Report on Research 2013 Under Sponsorship of the ACS Petroleum Research Fund

This ACS PRF grant supported two research thrusts in our lab related to the properties of colloidal suspensions in confined geometries. While the primary thrust of our work was to investigate solidification of concentrated attractive suspensions of micron-sized particles in thin geometries, we also applied techniques and algorithms developed in our primary thrust to study slowing of dynamics of nanoparticles diffusing in nanopost arrays. Confinement in both cases induced similar physics: as the suspensions were increasingly confined, the dynamics of the particles became increasingly solid-like. Remarkably, this was true even for the dilute nanoparticle dispersions, as long as they were highly confined. Below, we describe our major accomplishments over the past year.

(1) Dynamics of confined mixtures of monodispersed colloids and polymers

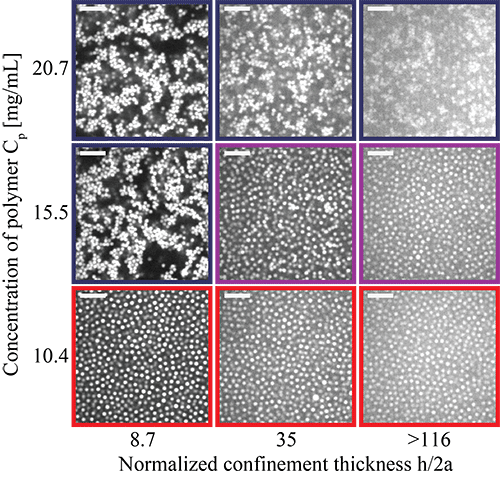
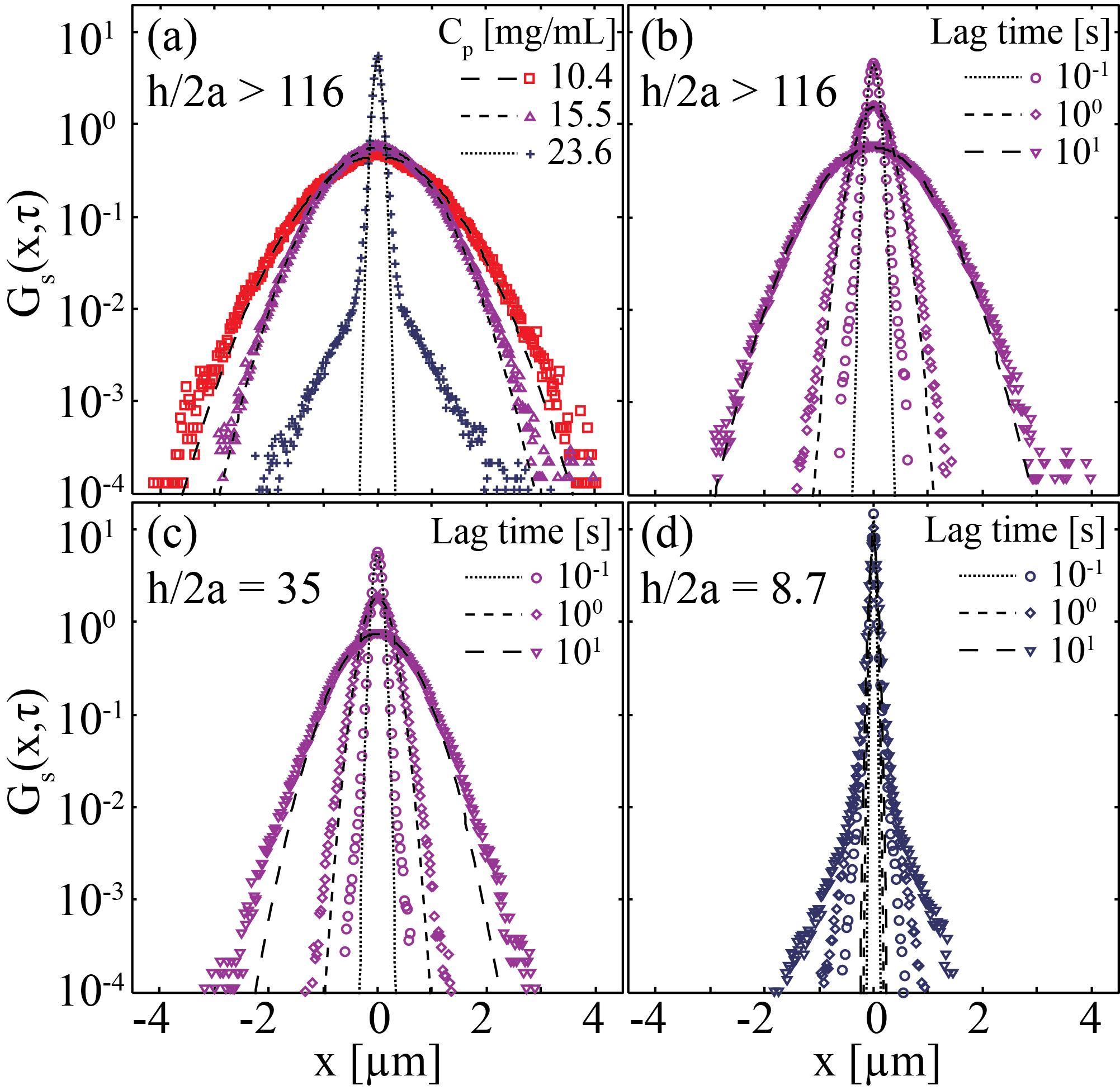
As models of attractive colloidal suspensions, we studied suspensions of micron-sized poly(methyl methacrylate) particles and non-adsorbing depletant polystyrene polymers in low-dielectric-constant solvents; the polymers induced an entropic depletion attraction between the colloidal particles. Using confocal microscopy and particle tracking, we measured mean-squared displacements and distributions of displacements of particles in mixtures in which particle volume fraction and polymer concentration were held constant, and showed that confinement in a thin wedge chamber induced slowing of the particle dynamics. Comparison with micrographs of samples at different confinement thicknesses indicated that slowing of particle dynamics was driven in part by clustering of particles en route to gelation. Figure 1 shows that as either the strength of the interparticle attraction (parameterized by the concentration of depletant polymer) or the confinement was increased, the suspension became increasingly solid-like, as indicated by the formation of large aggregated of particles. In both weakly- and strongly- attractive mixtures we also observed confinement-induced slowing of dynamics, suggesting that additional mechanisms beyond clustering and solidification contributed to changes in dynamics of confined colloid-polymer mixtures. Figure 2 shows that the distributions of particle displacements became increasingly non-Gaussian as either the strength of attraction was increased or as the confinement was increased, again consistent with the increasingly solid-like behavior.

Figure 1: Representative confocal micrographs of colloid-polymer samples at constant colloid volume fraction φ = 0.15 and varying concentration of polymer C_p and confinement thickness. Top row: C_p = 20.7 mg/mL; middle row: C_p = 15.5 mg/mL; bottom row: C_p = 10.4 mg/mL. The color of the border around each micrograph indicates the phase: fluid (red), fluid of clusters (purple), or gel (blue). Scale bars: 10 μm.

Figure 2: (a) Self-part of the van Hove correlation G_s(x,τ) at Τ = 10 s for bulk (h/2a > 116) samples with concentration of polymer C_p = 10.4 mg/mL (fluid, red) and 15.5 mg/mL (fluid of clusters, purple) in bulk and for C_p = 23.6 mg/mL at confinement thickness h/2a = 67 (gel, blue +). Lines indicate fits to single Gaussian functions. (b)-(d) G_s(x,τ) for C_p = 15.5 mg/mL sample at confinement thickness (b) h/2a > 116 (fluid of clusters), (c) h/2a = 35 (fluid of clusters), and (d) h/2a = 8.7 (gel) at varying lag times. Lines indicate fits to single-Gaussian distributions. Colors indicate the phase as in Figure 1.

(2) Dynamics of confined mixtures of bidispersed colloids and polymers

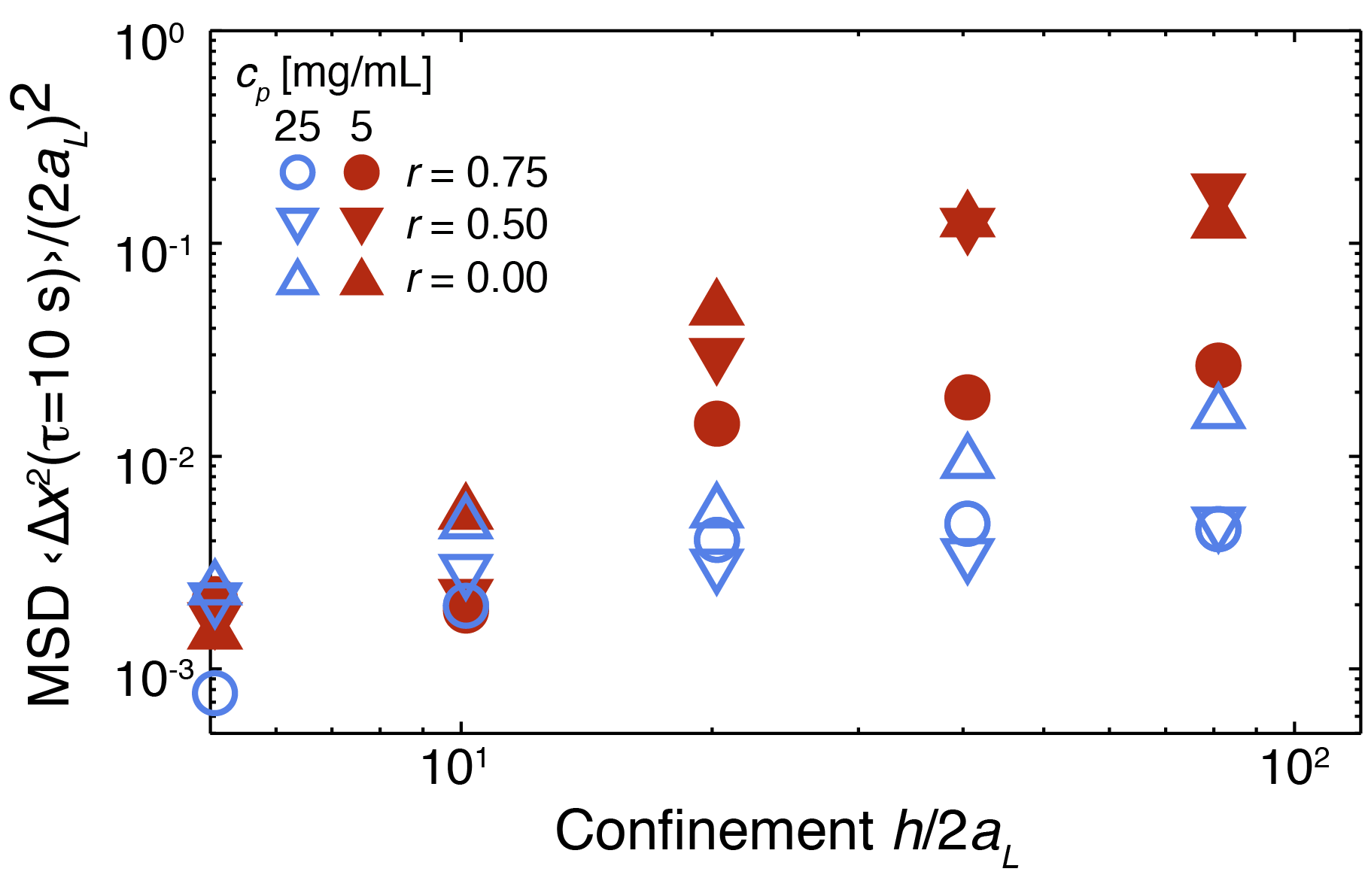
As an extension of the previous work, we investigated the effect of confinement on solidification of mixtures of non-adsorbing polymers and bidispersed colloidal particles (size ratio a_{S /} a_L ≅ 0.49) in a low-dielectric-constant solvent. Holding the total volume fraction of particles fixed, the dynamics of the large particles became increasingly slow as either the volume ratio of small particles was increased or the confinement thickness was decreased. Confinement to ten large particle diameters induced gelation in all samples investigated, with the most arrested dynamics appearing when both the depletant concentration and volume ratio of small particles were large, as shown by the magnitude of the mean-squared displacement at a fixed lag time in Figure 3. To elucidate the mechanism driving solidification, we investigated the effect of confinement on the electrostatic interactions between the particles in the low-dielectric-constant solvent. We found that the changes in dynamics were consistent with an increase in the effective interparticle attraction, driven by changes in the electrostatic repulsion between particles as the suspension was confined. This result suggests that even small changes in the number of charges on particles or in solvents of low dielectric constant can drive macroscopic changes in interparticle interactions and the resulting suspension phase behavior.

Figure 3: Normalized mean-squared displacement at a lag time Δt = 10 s of large particles as a function of confinement h/2a_L for binary suspensions with concentration of depletant polymer C_p ≅ 5 mg/mL (closed symbols) and C_p ≅ 25 mg/mL (open symbols) for varying volume percent of small particles r of 0.75 (circles), 0.50 (down-pointing triangles), and 0 (up-pointing triangles).

(3) Diffusive dynamics of nanoparticles in arrays of nanoposts

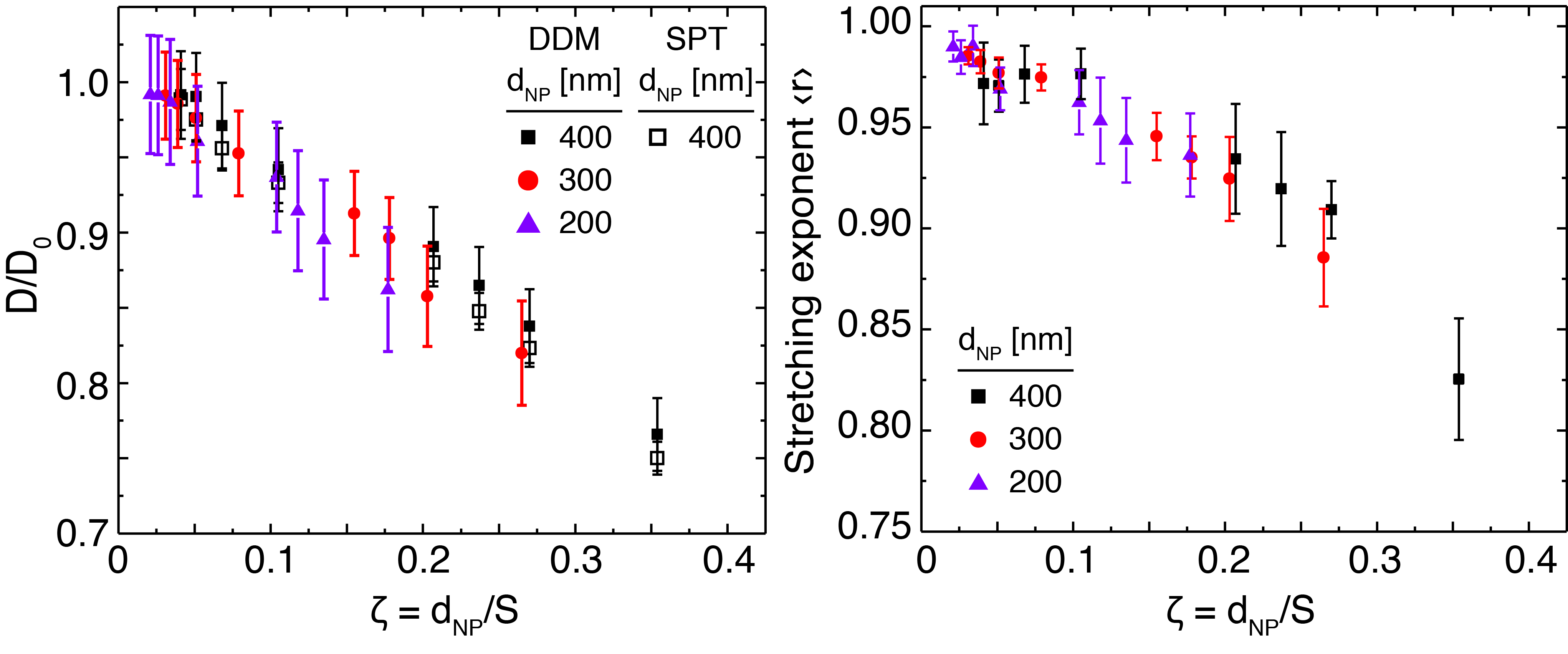
We studied the dynamics of dilute dispersions of nanoparticles of diameter 200-400 nm diffusing in square arrays of nanoposts. We applied particle-tracking algorithms to validate the dynamical measurements obtained using a new image-analysis technique, different dynamic microscopy. As the spacing between posts was decreased, the dynamics of the nanoparticles slowed. Moreover, the dynamics at all length scales were best represented by a stretched exponential, characterized by a stretching exponent r, rather than a simple exponential. Figure 4 shows that both the diffusivity of particles relative to their free diffusivity D/D₀ and the stretching exponent decreased linearly with increased confinement. Data for varying particle diameters (d_NP) and varying nanopost spacings (S) could be collapsed onto a master curve using a dimensionless confinement parameter ζ = d_NP/S. The slowing of the overall diffusive dynamics and the broadening distribution of nanoparticle displacements with increased confinement were consistent with onset of dynamic heterogeneity and approach to vitrification. Our results thus suggested that extreme confinement may give rise to arrested dynamics akin to those seen in colloidal glass transitions.

Figure 4: (a) Normalized diffusion coefficient D/D₀ and (b) average stretching exponent r (describing the distributions of displacements) as a function of dimensionless confinement parameter ζ = d_NP/S.