58th Annual Report on Research 2013 Under Sponsorship of the ACS Petroleum Research Fund

Since the start of award period, we have made progress on two fronts: determining the Tolman length for the intrinsic liquid-vapor surface and developing a more general formulation of density functional theory for curved surfaces.

The standard approach in describing the free energy of a curved surface is to expand the radius-dependent surface free energy density s(R) in powers of the curvature (1/R). For a spherical drop, this takes the form,

     ,                                                                 (1)

where s₀ is the surface tension of a planar interface, d is the Tolman length, and k and`k are known collectively as the rigidity constants. The work that we have accomplished during the first year of the award period focused on determining the constants d, k, and`k for a system of Lennard-Jones particles.

Firstly, we have performed simulations of a planar, liquid-vapor interface. The density profile of this interface – how the density varies as one goes from deep in the liquid phase to deep in the vapor phase – is thought to be composed of an intrinsic density profile that moves back and forth due to the effects of capillary waves. The capillary waved in effect broaden or smear out the density profile, and it is this broadened density profile that is typically reported in Molecular Dynamics simulations. One goal of this work is to eliminate the effects of capillary waves in broadening the liquid-vapor interface, examine the resulting intrinsic density profile, and determine how the Tolman length depends on this profile. To do so, we have developed criteria for robustly and uniquely locating the Gibbs dividing surface in the interfacial region. As described in the original proposal, we formally divide up the simulation box into a series of columns, each column spans the length of the box perpendicular to the interface (the z-direction) but is only a molecular diameter wide in the other directions. We determine the density profile r(z) within each column and apply a crossing constraint – when the density profile crosses a value of r_c = 0.5(r_l – r_v) – to determine the Gibbs dividing surface. r_l and r_v are bulk liquid and vapor densities, respectively. The resulting intrinsic density profile is shown below (solid line) with the capillary-wave-broadened profile (dashed line) for comparison.

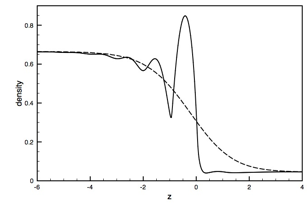As expected, the capillary-broadened interface has a significantly thicker interfacial region. The intrinsic profile shows oscillations in the density reflecting a layered structure near the interface. The existence of these oscillations in the liquid phase have been seen before, but their extension into the vapor phase is new. The decrease in density immediately on the vapor side of the interface represents a depletion layer. This is due to particles in the region feeling a stronger attraction from the higher-density liquid phase than lower-density vapor phase. Curiously, there is a small peak in the density profile in this region at about z = 0.8. We do not yet fully understand this peak, but suspect it is due to particles on the vapor side of the interface being temporarily prevented from being absorbed into the liquid phase by the presence of a liquid particle immediately beneath it.

In addition to determining the intrinsic density profile, we have also calculated the Tolman length, d, using the intrinsic interface. The Tolman length is related to the first-order coefficient in an expansion of the surface free energy in power of the curvature, as shown in Eq. (1). It is now generally agreed upon that the Tolman length is negative and is equal to d = -0.1 in units of the molecular diameter. Molecular Dynamics simulations of planar interfaces have reported positive values for the Tolman length and the source of this discrepancy remains unclear. We have applied a similar methodology to the calculation of the Tolman length as to that of determining the intrinsic density profile and the resulting values for d are indeed negative and range from -0.2 to -0.07. However, this calculation is very sensitive to the details of the methodology and we do not yet have a precise value for the Tolman length.

Secondly, we have developed new expressions for the bending rigidity k and Gaussian rigidity`k. Both of these constants are necessary to fully describe the surface free energy of a curved surface. These expressions feature a non-local integral term that accounts for the interaction between molecules. We have used these expressions to investigate the influence of the choice of the Gibbs dividing surface for a one-component fluid. The location of the dividing surface is a key element in our calculations of the Tolman length described above. The value of the Tolman length is independent of the choice of dividing surface. However, the value of the rigidity constants is not.

We have shown that when one chooses the equimolar dividing surface for the Gibbs dividing surface, the values of the rigidity constants are each at an extremum: the bending rigidity k is at its maximum and the Gaussian rigidity`k is at its minimum.

We have explicitly calculated both k and`k using a short-ranged potential and determined that k is negative and has a value around minus 0.5-1.0 k<sub>B</sub>T and`k is positive and has a value that is a bit more than half the magnitude of k.

In the coming year, we plan to finalize the methodology for calculating the Tolman length from our simulations of planar interfaces and then explore the temperature dependence of d. We will also use this methodology to explore the discrepancy between the known negative value for d and the positive values that have been calculated using Molecular Dynamics simulations. We hope to have an understanding of this origin of this discrepancy by the end of the second year of the award. We will also introduce a second species into our simulations and begin to investigate the behavior of the surface free energy in systems that contain surfactant or nanoparticles.