46108-AC6
Ion Evaporation from Taylor Cones of High-Conductivity Electrolytes Immersed in Hydrocarbons
We have progressed through the following fronts
1. Charge injection into non-polar liquids from electrosprays of highly conducting liquids
In the midst of a small cell filled with heptane we introduce a capillary needle through which we inject the conducting liquid to be electrosprayed (figure 1). The electrospraying liquid has very high electrical conductivity, and by analogy with what we find in vacuum, we hope to inject ions, rater than small drops. We have used two very different highly conducting liquids: salty water and the ionic liquid (IL) ethylmethylimodazolium tetrafluoroborate (EMI-BF4). The system is working very well. We have measured electrospray current I versus liquid flow rate curves I(Q), from which we infer mean charge/mass (q/m) ratios for the emissions. q/m does not correspond to ions, but to larger drops. We estimate their size by assuming that they are charged near the Rayleigh limit, which gives us a range of radii about 5 nm. This is initially disappointing result is preliminary, and a systematic exploration of other conductor-dielectric combinations remains to be performed.
Fig. 1: Electrospray of saline
water into a heptane bath from a sharpened silica capillary In water electrosprays water
bubbles form at the collector. But not for ILs due to its slight solubility in
heptane. This means that our IL drops, initially 10 nm in diameter, dissolve
and release the ions, exactly as in conventional ESI in air. To confirm this
crucial point more directly we have started the proposed effort to measure
mobility distributions as proposed, in a differential mobility analyzer (DMA).
We have initially tried to implement a time of flight approach, with some
preliminary success. 2. Electrospraying of heptane
for the analysis of petroleum products Our approach is to inject charge
inside heptane from an ES of EMI-BF4 (Figure 2). It works
surprisingly well. In collaboration with Professor Gomez we have made
preliminary measurements of the electrospray current and drop size for these
heptane drops.
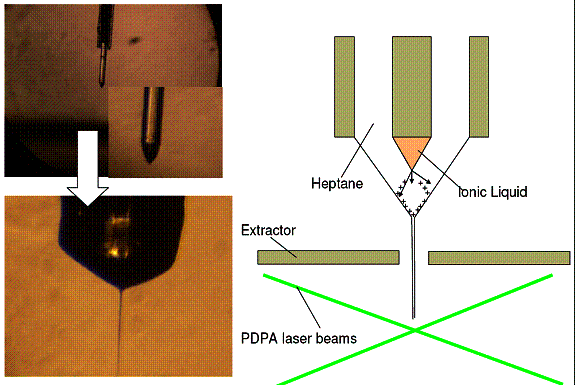
Figure 2: compound electrospray of a Taylor cone of the ionic liquid (IL)
EMI-BF4, inside a capillary containing heptane. The charge injected
into the heptane by the electrospray of IL goes to the heptane-air interface,
makes it unstable, and ejects an electrospray of heptane (lower left). The top
left image shows the Taylor cone of IL emerging outside the larger capillary
(containg the heptane), and electrospraying into air. The bottom image shows
the heptane air interface with a heptane jet. 3. Miniature Differential
Mobility Analyzer (DMA) for ion mobility measurements inside a dielectric
liquid. We have already built and tested a Differential Mobility
Analyzer (DMA) with which we expect to see discrete mobility spectra for the
ions injected into the dielectric liquid (figure 3). The instrument is similar
to others of which we have built many over the years for mobility analysis in
the gas phase. But it has much smaller dimensions in the separation chamber (2
mm gap between electrodes) to accommodate the much smaller associated ionic
mobilities. Based on the time of flight measurements already mentioned, we know
that electrical drift velocities will be adequate for the instrument to run at
practical convective velocities. Using tetraheptylammonium ions in air this DMA
has demonstrated a resolving power of 50.
Figure 3: Handheld
DMA for analysis of ions inside a dielectric medium.
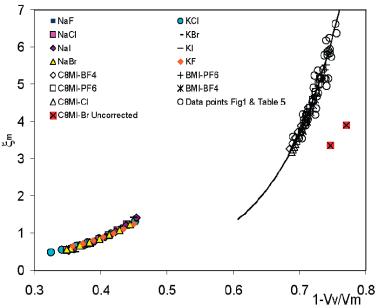
4. Correlation of properties of ionic liquids with void fraction Ionic liquids are an essential component of our ion injection work, and
their physical properties (particularly the surface tension g) have a strong effect in the ability to
extract ions from the IL. We have therefore sought schemes to anticipate g. Furth's cavity theory, suggests that the dimensionless
number x=g(V++V-)2/3/kT
formed with g, the thermal energy kT and the sum of anion
and cation volume V++V- (based on their crystallographic
radii obtained from X ray diffraction), is a constant. For ionic liquids we
find rather that g(V++V-)2/3/kT
is a function of the void fraction xv, defined as 1 - (V++V-)/Vm,
where Vm is the molecular volume based on the bulk density of the
IL. This simple hypothesis succeeds remarkable in capturing the behavior of all
ILs (many dozens) at all temperatures for which data are available. Figure 4
shows this for both inorganic molten salts and ionic liquids. One figure in
this article has made it to the cover of the current issue of J. Phys. Chem. B.
Figure 4: Correlation between the surface tension variable x = gVm2/3kT
vs. the fraction of the liquid occupied by anions or cations, (V++V-)/Vm. [1]