62nd Annual Report on Research 2017

Introduction

The eventual goal of this project is to develop a novel interatomic potential that will enable atomic-scale simulations for the structure and thermodynamics of calcium carbonate (CaCO₃) pre-nucleation clusters in water. To do this, we need benchmark information on the hydration of the CaCO₃(aq) contact ion pair, which is not available. Thus, we first establish the structure and energetics of CaCO₃(aq) hydration using first-principles techniques.

Progress to date

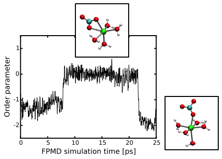
Previously, we found that the structure of hydrated CaCO₃(aq) as derived from classical molecular dynamics (MD) with model interatomic potentials [1] disagreed with first-principles MD using density functional theory (DFT) and the generalized gradient approximation (GGA). The classical MD predicted a 7-coordinate Ca²⁺ complex with six waters plus a carbonate coordinated in a monodentate fashion. In contrast, first-principles MD gave a 6-coordinate Ca²⁺, where the carbonate coordination shifts between mono- and bidentate on the time scale of the simulation (Figure 1).

Figure 1: Dynamics of the order parameter from first-principles MD simulation of CaCO₃(aq), defined as the difference in the Ca²⁺ and carbonate oxygen distances. An order parameter of ~ 0 corresponds to bidentate coordination; a non-zero order parameter represents monodentate coordination. One the time scale of the simulation (~ 30 ps), the carbonate coordination switches between monodentate with five waters of hydration around Ca²⁺, and bidentate carbonate with four waters of hydration.

However, there are well-known weaknesses in the DFT-GGA description of liquid water and metal ion hydration [2]. In order to confirm the first-principles MD findings, we embarked on a complementary approach to study metal ion hydration using finite cluster models, which can be treated using quantum chemical techniques and Gaussian-type basis sets. Such models permit the use of a wider variety of DFT functionals (i.e., hybrid functionals) that are not possible in first-principles MD, which rely primarily on plane-wave basis sets and the GGA.

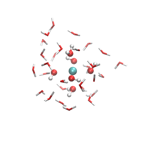
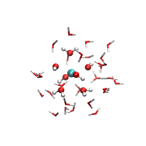
We have approached this with a simpler system, the hydrated Ce(OH)₄(aq) complex, employing DFT with the hybrid exchange-correlation density functional PBE0 [3]. A preference for a particular hydration environment can be established by comparing the energetics of different coordination structures; in this case, we have optimized clusters of 6, 7, and 8-coordinate Ce⁴⁺ (Figure 2). Such cluster models require at least two complete solvation shells, which correspond to a minimum of about 30 water molecules. Future work will apply this cluster approach to establish the preferred hydration structure of CaCO₃(aq).

Figure 2: Finite cluster models for the hydrated Ce(OH)₄(aq) complex. Clusters have varying coordination numbers (CN) have been optimized: 6-coordinate (left), 7-coordinate (middle), and 8-coordinate (right). In order to compare their energetics, one has to take care that each cluster is constructed to have the same number of hydrogen bonds to ensure proper cancellation of errors.

Impact

The ACS-PRF award has supported a total of two graduate (MS) students and two undergraduate (BS) students. Two of these students have graduated and successfully transitioned to jobs in industry; a third student is expected to graduate later this year and is applying to pursue a Ph.D. in chemistry.

References

[1] Raiteri, P.; Gale, J.D.; Quigley, D.; Rodger, P.M. Derivation of an Accurate Force-Field for Simulating the Growth of Calcium Carbonate from Aqueous Solution: A New Model for the Calcite-Water Interface. J. Phys. Chem. C 2010, 114, 5997–6010. DOI: 10.1021/jp910977a

[2] Gillan, M.J.; Alfe, D.; Michaelides, A. Perspective: How good is DFT for water? J. Chem. Phys. 2016, 144, 130901. DOI: 10.1063/1.4944633

[3] Perdew, J.P.; Ernzerhof, M.; Burke, K. Rationale for mixing exact exchange with density functional approximations. J. Chem. Phys. 1996, 105, 9982. DOI: 10.1063/1.472933