62nd Annual Report on Research 2017

The goal of this project is two-fold: (1) develop a continuum level model for shear thickening fluids suitable for complex flow simulations, and (2) develop a numerical tool capable of simulating these complex flows.

1   Model for Shear Thickening Fluids (STFs)

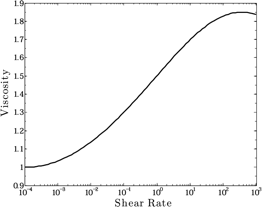
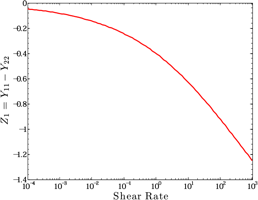
We have focused our attention on a model for particulate suspensions that has been tested against particle dynamics simulations and experimental data, namely the model by Stickel, Phillips and Powell (SPP) [1]. The SPP model governs the evolution of a tensor that describes the local structure of a particle suspension, defined as the inverse of the mean-free path length, upon which the particle stress is dependent.  We have identified parameter spaces in which the model is capable of predicting shear thickening, Figure 1, similar to experiment [2].  The model suggests that the thickening is due the clustering of particles perpendicular to the flow as seen in the dominance of the 22-component of the structure tensor, Figure 2.  We have subsequently subjected the model to 1D channel flow simulations.  We accurately predict the triangular-like velocity profiles, typically seen in flow of STFs, as well as a decrease in the volumetric flow rate relative to Newtonian fluids at the same pressure drop.

Figure 1 Viscosity vs. shear rate showing the capability of the SPP model to predict shear thickening.

Figure 2 Difference between the 11 and 22 components of the structure tensor.  The negative value indicates particles are clustered perpendicular to the flow.

The question we ultimately seek to answer is how these flow phenomena affect more complex, industrially-relevant flows. Before tackling this question, we consider the fact that most complex flows contain a strong extensional flow component.  We have thus tested the model under homogeneous planar extensional flow.   Simulations of the SPP model, within the STF parameter spaces, captures the extensional thickening observed in extensional flow experiments [2], Figure 3.

Figure 3 Viscosity vs. extension rate showing the capability of the SPP model to predict extensional thickening.

2   Complex Flows

Concurrent with the investigation of a model for STFs, we have been focused on simulations of models that describe complex fluids under complex flow conditions, e.g., flow in a cross-slot and around a 90-degree bend. In order to simulate flows in these complex geometries, we have implemented several constitutive equations in the viscoelastic solver viscoelasticFluidFoam [3], which can be found in the extend version of OpenFOAM¨ (version 3.0).  While the SPP model is currently being considered under purely shear and extensional flows, we have focused our complex flow simulations on well-developed models for polymer and wormlike micellar solutions.

In cross-slot flow, we have conducted simulations of the VCM model [4] in order to investigate the role chain scission plays in altering flow.  In our recently published work [5], we have shown that the breakage of micelles can lead to secondary flows that would otherwise not be present in the absence of chain scission, Figure 4.  We are currently delving deeper into the role chain scission plays on this secondary flow as well as on elastic instabilities.

Figure 4  Close-up of the contour plots of the number density of long wormlike chains with streamlines clearly showing the recirculation region due to chain breakage.

In the flow around a bend we have considered several different models for polymers, each of which predicts different shear and extensional rheology.  We have thus far discovered shear thinning is a necessary condition for the formation of vortices along the inlet channel wall (prior to the bend) in agreement with experimental work [6].  Going one step further, we have shown that shear thinning is not a sufficient condition - as the degree of shear thinning increases, the secondary flow is suppressed, Figure 5.

Figure 5 Close-up of the lip vortices for the FENE-P model in the flow around a 90-degree bend. The different streamline colors represent different degrees of shear thinning, with green representing the more shear thinning polymer.

3   Impact

The support from this grant has provided research opportunities for seven undergraduate students from varying backgrounds (mathematics, chemical engineering, mechanical engineering, and physics).  Each of the students gained valuable experience in rheology and viscoelasticity, programming (via Matlab and OpenFOAM), and in differential equations.  All students have presented at the RIT Undergraduate Research Symposium, and one student gave a poster presentation at the annual Society of Rheology meeting in Tampa, FL.  This latter student is the lead author on our publication on the flow of wormlike micelles [5], and plans to attend graduate school next year, pursuing a Ph.D. in computational mathematics.

The PI has gained significant experience in mentoring student research, and now currently supervises six undergraduate research students.  The support from this grant has enabled the PI to present at the 2017 annual meeting of the Society of Rheology in Tampa, FL, and at the 18^th International Workshop on Numerical Methods for Non-Newtonian Flows in Vancouver, BC, CA.  Publications are being prepared based upon the work on flow of polymers around a bend, on the SPP model for shear thickening fluids and, and on the more detailed study of the elastic instability and secondary flow in cross-slot flow of wormlike micelles.

4   Future Work

With the SPP model showing promise as a model for STFs, in particular, simultaneously predicting the shear and extensional rheology, and with the numerical solver showing an ability to tackle complex mathematical models and flow phenomena, we have the capability to marry these projects.  In addition to further study of the flow of polymers and wormlike micelles, we will begin to provide detailed studies of both the macro and micro flow behavior of STFs in complex, industrially-relevant geometries.

References

[1] Stickel et al., J. Rheol. 2006, 50, 379-413

[2] Chellamuthu et al., Soft Matter 2009, 5, 2117-2124

[3] Favero et al., J. Non-Newtonian Fluid Mech. 2010, 165, 1625-1636

[4] Vasquez et al., J. Non-Newtonian Fluid Mech. 2007, 144, 122-139

[5] Kalb et al., Phys. Rev. Fluids 2017, 2, 071301

[6] Gulati et al., J. Rheol. 2010, 60, 375-392