62nd Annual Report on Research 2017

Introduction and Objectives

Increasing energy costs have attracted oil companies to tap into heavy crude oil reserves. Heavy crude oil is a colloidal suspension of aggregates of many compounds (resins and asphaltenes), which give rise to very unusual rheological properties such as non-Newtonian behavior and very high viscosity. Such high viscosity leads to difficulties in the production/transportation of heavy crude oil. To optimize processes to lower viscosity and improve flow properties of heavy crude oil, a better understanding of the relationship between micro-structure and macro rheological behavior is required. Here we propose to study the effects of micro-structure (size, shape, polydispersity, concentration, etc.) on the rheology of heavy crude oil using state-of-the-art numerical simulations without the simplifying assumptions of previous theoretical models.

Methods

We use our well-validated, sharp-interface immersed boundary method to simulate colloidal suspensions of asphaltene with their experimentally observed micro-structure. We have incorporated the methods for calculating the particle stresses that affect the bulk stress of the suspension, from which the effective viscosity of the suspension is determined (Fig. 1). Moreover, we separately calculate different terms affecting the bulk stress, to identify the relative importance of different mechanisms of stress generation in the suspension.

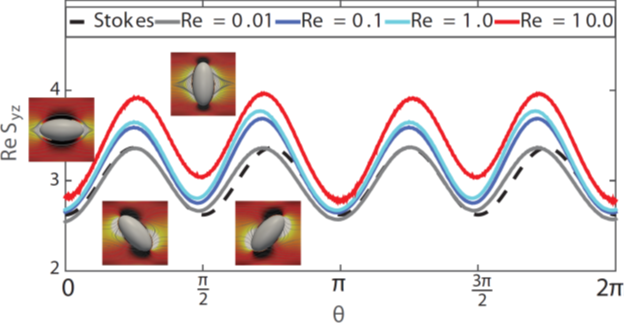
Figure 1 Validations: The stresslet of an ellipsoid as a function of orientation θ at different Re compared with the Stokes solution. The insets show the streamlines and the vorticity around the ellipsoid at θ = 0, π/4, π/2, and 3π/4, respectively.

Our results show that a particle's shape can increase the particle stress by more than 50% relative to an equivalent axisymmetric particle-see next section. Therefore, we are extending our current numerical tools to simulate flows with many particles. The main challenge in simulating many particles with irregular shapes is identifying and modeling their collisions. In contrast to spherical particles, the collision of irregularly shaped particles cannot be determined just by the distance between their centroids. In our method, the collision is detected when the distance between two particles is smaller than a threshold. The distance between the particles are computed based by calculating the distance between their nodes they are discretized with. We use bounding box and control cell strategies to reduce the computational cost of this method. After we identify colliding particles, we need a strategy to model the collision. Here we model collision based on their coefficient of restitution by correcting the linear and angular velocities of the particles.

Results

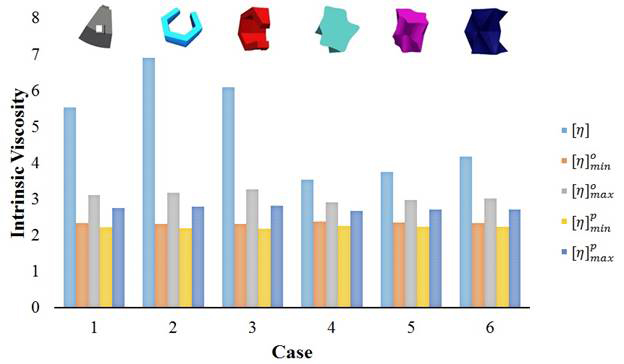
The irregular shape of particles in suspensions is typically approximated by simple geometries such as spheres or ellipsoids. We investigated the accuracy of such an approximation by comparing two irregular-shaped particles with different initial orientations against their equivalent spheroids in dilute volume fractions. The shape of the particles and their initial orientation is shown on the top of Fig. 2. Our results show that the average shear particle stress (and also intrinsic viscosity) of irregular particles can be 20 to 120% higher than the maximum value of their geometric or kinematic equivalent spheroidal particles, and closer to spheroids with higher aspect ratios (Fig. 2).

Figure 2 The intrinsic viscosity [η] of an irregular particle in comparison with that of equivalent oblate [η]o and prolate [η]p spheroids at minimum and maximum orbits. The intrinsic viscosity of suspensions for irregular particles are about much larger than equivalent spheroids.

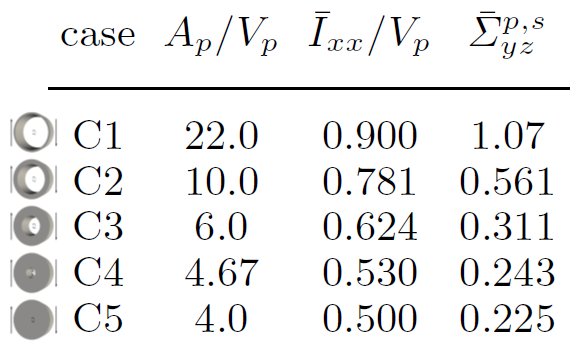
We found that two geometric factors of an irregular shape, i.e., surface to volume ratio and moment of inertia per unit volume, are correlated with the particle stress. In fact, the shear particle stress of a ring-shaped particle, which has a very large value of these factors, is five times larger than its equivalent spheroid. The correlation of these geometric factors with particle stress is further confirmed by considering two families of shapes (cylinder- and sphere-like particles). Fig. 3 shows the results for the family of cylinder-like particles.

Figure 3 Simulations of a family of cylindrical shapes (C1=ring to C5=cylinder) in dilute regime with varying surface-to-volume ratio (Ap/Vp) and moment of inertia per unit volume (Ixx/Vp) show that increasing these parameters increases the particle stresslet (right column) and consequently suspension viscosity.

We also found that acceleration stress and especially Reynolds stress (stress mechanisms due to inertia) can have comparable average values with the stresslet term and effectively increase and decrease the absolute value of the first normal stress difference N1 and second normal stress difference N2, respectively. However, their contribution to the shear particle stress is negligible. Our results pave the way to define better equivalent particles for irregular ones.

Conclusions

We found that despite qualitative similarities between the rotation of an irregular-shaped particle and a spheroid, irregular-shaped particles have a more complicated rotation behavior. Depending on their initial orientation, a complex kayaking motion with significant cycle-to-cycle variation can be seen for both particles. Our results show that the particle stress depends on both initial orientation and particle shape, and its value can considerably change when particles rotate in different orbits. Based on our calculations for two irregular particles, the average shear particle stress is 20 to 120% higher than the maximum value for their equivalent spheroidal particles, and it is closer to spheroids with higher aspect ratios. Therefore, the current methods of defining equivalent particles for irregular ones underestimate rheological properties. Our results can lead to better equivalent models for irregular particles in the future.