print pageprinter friendly
Reports: DNI956107-DNI9: Dynamic Discrepancy Reduced Modeling for Adaptive, Multi-Model, Nonlinear Model Predictive Control

David S. Mebane, Ph.D., West Virginia University

October 2, 2017

The project goal is the development of a reduced model for the Fischer-Tropsch reaction using the dynamic discrepancy (DD) methodology, and the subsequent incorporation of that model into a reactor-scale model. A significant part of the project is the development of the detailed methodology and computational framework that will enable this. It is the development of these aspects of the program – as well as the training of students – that has occupied the first year of the project.

Consider the high-order dynamic system

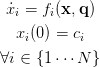˙xi = fi(x,q ) xi(0) = ci ∀i ∈ {1⋅⋅⋅N }

(1a)

(1b)

(1c)

representing a chemical reaction (such as Fischer-Tropsch). An associated process model depends only on a subset of M ≪ N states. These states correspond to an M-dimensional dynamic system

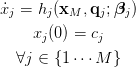x˙j = hj (xM ,qj;βj) xj(0) = cj ∀j ∈ {1⋅⋅⋅M }

(2a)

(2b)

(2c)

DD is a method of finding a stochastic version of the system (2) that reproduces the dynamics of the full system for the reduced set of states.

Assume that the functional form of each fi in the system (1) is a composition of mass-action chemical rate expression with specified input / output flows q:

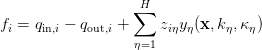∑H fi = qin,i - qout,i + ziηyη(x,kη,κ η) η=1 (3a)

where H is the total number of chemical reactions, ziη is the stoichiometry of the species xi in reaction η, and

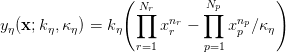( Nr Np ) y (x;k ,κ ) = k ∏ xnr- ∏ xnp∕κ η η η η r p η r=1 p=1 (3b)

where ki and κi are rate and equilibrium constants, nr,np ∈ ℕ0 are stoichiometries and Nr + Np = N. The form (3b) is advantageous because it prevents unphysical states (such as negative concentrations) from arising. The DD formulation thus retains this functional form:

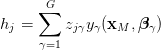∑G h = z y (x ,β ) j jγ γ M γ γ=1 (4a)

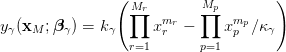(∏Mr M∏p ) yγ(xM ;β γ) = k γ xmr - xmp ∕κγ r=1 r p=1 p (4b)

where m and M correspond to n and N from (3b), respectively, and

kγ = exp [δk(xM ;βk γ)] κγ = exp [δκ(xM ;β κγ)]

(5a)

(5b)

where the discrepancy functions δ are Gaussian process stochastic functions of the BSS-ANOVA type. The DD method calibrates the reduced model to high-fidelity data using a Bayesian approach, thus tailoring the discrepancy functions to the available data.

Before the project started, a manuscript was prepared and submitted to a journal on DD reduced order modeling for a smaller system: the catalytic steam reformation of methane. A high-fidelity model1 was implemented in MATLAB and used to produce calibration data for a DD reduced order model, also implemented in MATLAB. A MATLAB-based Markov chain Monte Carlo (MCMC) sampler was used to calibrate the DD model to the high-fidelity data, and both high-fidelity and DD-based reduced order process-scale models were implemented for comparison. The comparison was successful (the DD process-scale results ’covered’ the high-fidelity result), but subsequently it was determined that a bug contained in the routines that evaluate the discrepancy functions rendered the results invalid. The study is thus in the process of being redone, with several improvements:

  1. A methodology has been established that will limit the number of terms in the expansion of the discrepancy functions, further enabling the functions to be determined in an automated fashion (machine learning)
  2. The reduced models and MCMC routine have been ported from MATLAB to C++
  3. Bachelor’s and Master’s level students have been trained in the mathematical and computational skills required for the project

Each of these developments are important milestones along the path of achieving the overall goals of the project.

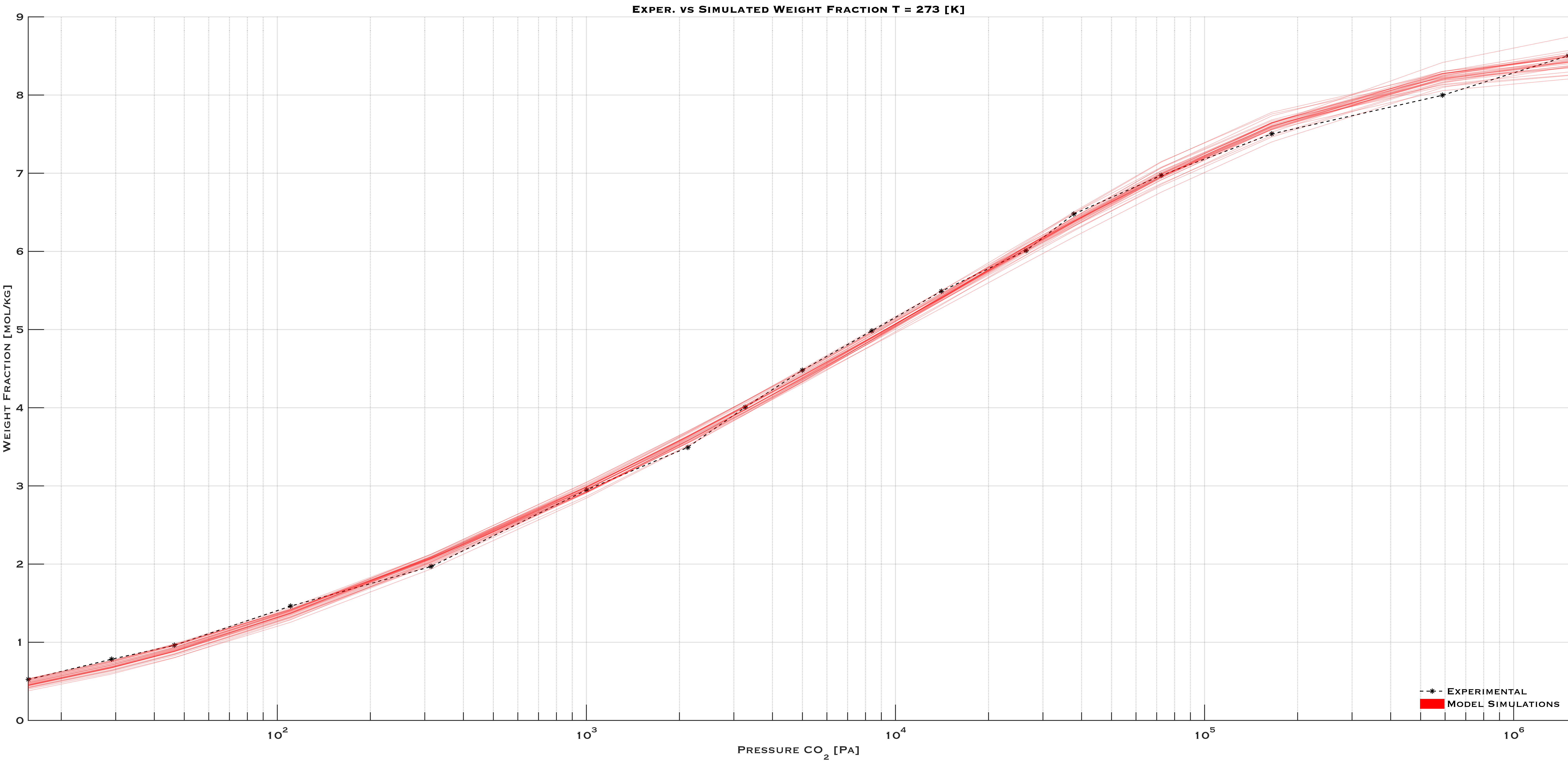
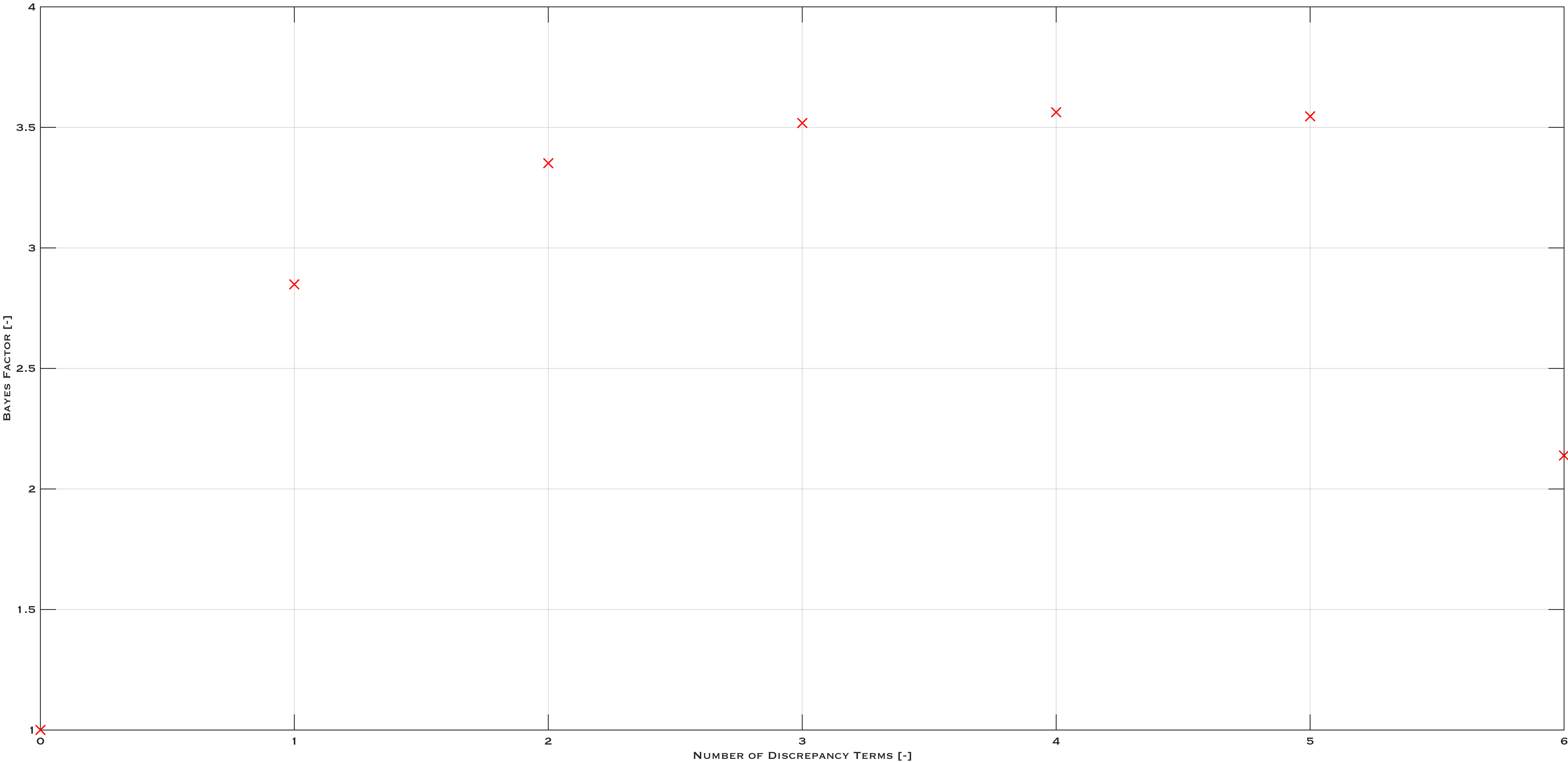
The first item in the list above was developed in the context of a discrepancy-based adsorption isotherm, the terms of which are determined by calibrating models to experimental isotherm data. The model starts with a Langmuir isotherm model, with an equilibrium constant functionalized with a discrepancy function as in (5b). Terms are added to the discrepancy in an automated fashion, until a metric (a “Bayes factor”) which balances model fidelity with model complexity, reaches a maximum. This work has been developed into a self-contained application called “IsoFit”, which will be publicly released.

pict

Figure 1: Experimental data2 (black asterisks) with model results (red lines) for the IsoFit tool.

pict

Figure 2: Bayes factor vs. number of discrepancy terms for the IsoFit tool, showing a maximum at four terms.

This strategy will be applied to both steam reformation and Fischer-Tropsch DD reduced models.

Current progress in the project is that the model for the steam reformation has been implemented in C++ and calibrations to high-fidelity data are in progress. A Master’s student joined the group approximately one year ago; has learned the DD theory (including both modeling and calibration aspects) along with the skills in Unix, C++ and parallel computing necessary to complete the work for both steam reformation and Fischer-Tropsch projects. We expect significant results over the next year.

In terms of my career, this project has been essential. My program is one of deep scientific inquiry into important problems in the energy sector, and the development of mathematical and computational tools required to utilize the results of those inquiries for models with engineering and industrial utility. This project has enabled me to sustain the critical latter part of that. It has enabled travel to meetings where I can find collaborators, make allies and identify potential funding sources. The project will also be instrumental in my tenure decision, which is coming next year. References

  1. Xu, J. and Froment, G. F. (1989), Methane steam reforming, methanation and water-gas shift: I. Intrinsic kinetics. AIChE J., 35: 8896.
  2. Pulin, A. L., Fomkin, A. A., Sinitsyn, V. A. and Pribylov, A. A. (2001), Adsorption and adsorption-induced deformation of NaX zeolite under high pressures of carbon dioxide. Russ. Chem. Bull., 50: 60-62.