62nd Annual Report on Research 2017

Objectives

The goal in this work is to develop novel computationally efficient operability-based approaches for the design of high-dimensional and nonlinear systems motivated by natural gas utilization processes. The developed approaches will employ extended classical operability concepts to attain process intensification towards system modularity. The catalytic membrane reactor for the direct methane aromatization conversion (DMA-MR) to hydrogen and benzene was chosen to be the initial case study. It consists of a nonlinear system whose design is challenged by complexity, including nonlinearities and a highly-constrained environment. Additionally, this system can be considered as a potential candidate for modular natural gas applications.

Aims and Results

Specific aim #1

Establish a multi-model operability approach for high-dimensional nonlinear systems

Our approach will involve high-dimensional linear operability calculations using linearized versions of the process model at different operating regions.

(i) Obtain Linearized Versions of the Process Model at Different Operating Regions

An initial study of the input-output spaces was carried out through extensive simulations, generating the available input set (AIS) and the achievable output set (AOS). In this study, sensitivity analysis was performed to provide a set of linearized models for the original nonlinear system. Using a computational geometry-based technique (Delaunay triangulation), the linear relationships from such models were translated to sets of triangles, in which each triangle in the AIS had a counterpart in the AOS. This method was repeated with a gradual reduction in number of points considered, until the triangulation was still possible for the minimum number of points/models.

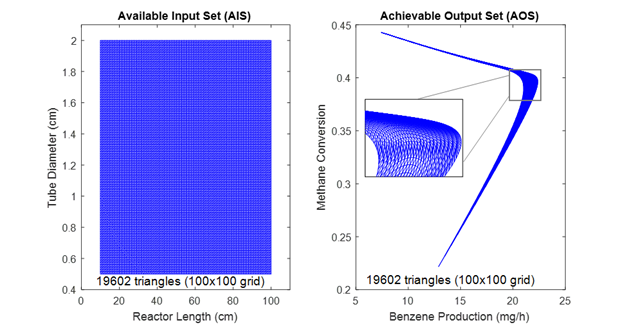
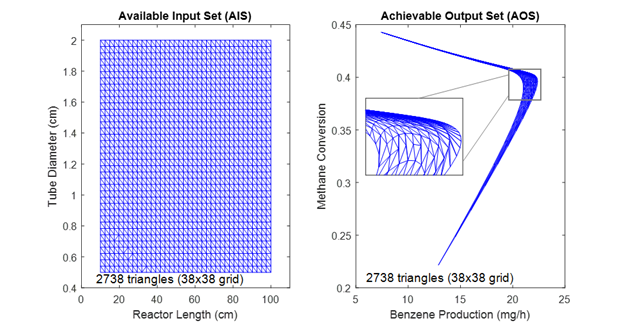
For the DMA-MR system, two design variables were selected as inputs (reactor length and tube diameter), whereas two performance variables were selected as outputs (benzene production and methane conversion). As shown in Figures 1 and 2, the number of triangles required for the representation of this 2x2 system presented a reduction of about 86% after the implementation of the proposed approach.

Figure 1. AIS and AOS result for the initial case.

Figure 2. AIS and AOS result for the case with minimum number of triangles.

The future work in this task will consist of the further analysis of the mathematical relationships between triangles and linearized models and the inclusion of process disturbances.

(ii) Quantify the Operability Spaces for the Linearized Models using a Multi-model Operability Approach

The obtained relationship between AIS and AOS describes the behavior of the selected system by sets of triangles that link inputs and outputs. Using this relationship and the obtained triangles, the desired input set (DIS) computation was performed employing the Multi-Parametric Toolbox (MPT) in MATLAB ^[1]. To include additional targets related to process intensification and system modularity, an optimization algorithm based on mixed-integer linear programming (MILP) was formulated.

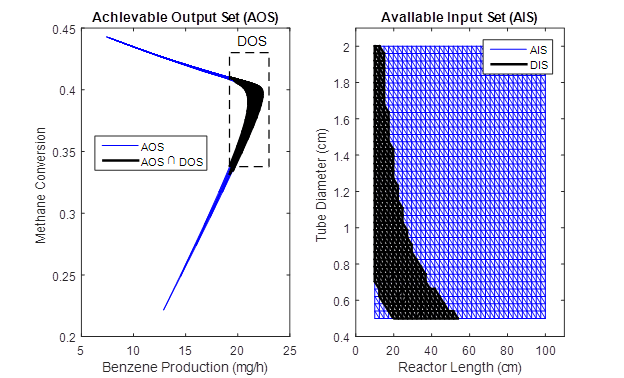
For the DMA-MR system, the intersection between the desired output set (DOS) and AOS portrays the extent of achievability in terms of benzene production and methane conversion, as illustrated in Figure 3. The DIS represents the necessary reactor dimensions to obtain this output operating region. Preliminary results of the MILP formulation indicated that the benzene production can be optimized, while the membrane reactor presents a reduction in 60% of volume (catalyst zone) and 80% of membrane area, thus enabling process intensification.

Figure 3. Calculation of AOS and DOS intersection and computation of DIS.

The next steps in this analysis will be to increase the system dimensionality and expand the limits of the AIS, considering physical process limitations.

Specific aim #2

Develop a fully nonlinear method for high-dimensional systems

Our approach will entail plantwide operability analysis employing computational geometry and nonlinear optimization tools.

(i) Introduce an Iterative Algorithm for the Analysis of High-Dimensional Nonlinear Systems in the Output Space

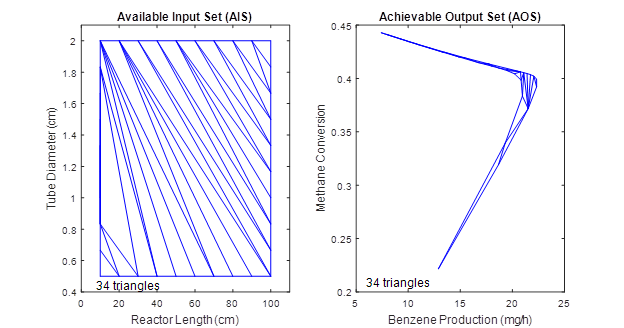
Previously employed techniques such as Delaunay triangulation can also be applied to describe the process operating envelope, with the advantage of a reduced requirement in the number of triangles and thus faster computational speed. Figure 4 shows the application of Delaunay triangulation to obtain the DMA-MR process operating envelope.

Figure 4. Calculated operating envelopes described by triangles.

As future work, the introduced computational geometry tools will be adapted to accommodate high-dimensional systems. The analysis of alternative geometry-based techniques involving other convex shapes will also be discussed if needed.

(ii) Develop a Nonlinear Optimization-based Approach for Computationally Efficient Operability Computations

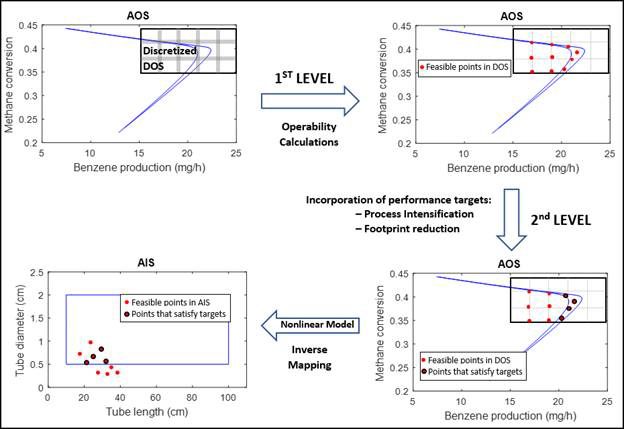
A nonlinear bilevel optimization framework was formulated to consider process nonlinearities and meet the requirements associated with process intensification and desired performance targets. In this framework, the first level ensures the achievement of the DOS through operability calculations. The second level enables the optimization of the feasible points obtained in the first level, towards identifying the optimum solution with respect to process intensification. As the last step, an inverse mapping computation indicates the necessary inputs to achieve the obtained outputs. A schematic diagram of this framework is depicted in Figure 5.

Figure 5. Schematic diagram of the nonlinear optimization-based framework.

Results indicated that the computational time of the formulated nonlinear optimization-based approach is strongly correlated to the initial discretization of the DOS, i.e., the number of initial points. This relationship suggests a tradeoff between accuracy and computational time that will be further analyzed as the next step. When applying this framework to the same 2x2 system of aim #1, similar membrane reactor size reduction and benzene production optimization were obtained.

Future Work

In the future, the incorporation of disturbances and the inclusion of more dimensions in the operability calculations will be considered for the specific aims #1 and #2. Additionally, other natural gas systems will be studied for simulation and development of specific aim #3.

Research Impact and Products

In addition to the scientific contribution, the research project has provided students with training in a wide range of process systems and computational tools, including the participation in conferences (AIChE, FOCAPO/CPC) and publications (see reported published articles acknowledging ACS PRF).

References Cited

[1] Herceg M., Kvasnica M., Jones C.N., and Morari M. “Multi-Parametric Toolbox 3.0”. In Proceedings of the European Control Conference, pages 502–510, Zurich, Switzerland, July 17–19 2013.