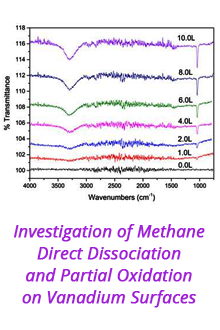
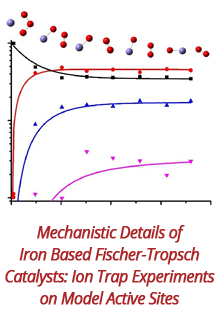
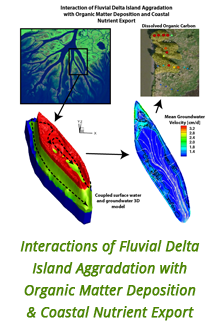
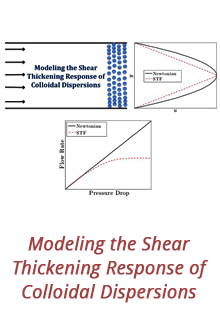
Reports: DNI655195-DNI6: Emergence of Entropy From the Mixing Dynamics of Complex Liquids
Jason R. Green, PhD, University of Massachusetts, Boston
Mixing matter and energy are responsible for the transport and transformation of chemicals in solution. One way to characterize the mixing process is with the thermodynamic entropy. However, predicting the thermodynamic entropy of mixing is a difficult problem for liquids composed of molecules with internal structure, dissimilar intermolecular interactions, or many components, features that are found in the complex hydrocarbon mixtures central to the petroleum field. This project aims to gain a new understanding of entropy, as it emerges from the dynamics of molecules, in liquids that are mixing. The theoretical framework we are applying uses statistical dynamical entropy measures, namely the KolmogorovSinai (KS) entropy rate, for
Liquids live in a state between the structural order typical of solids and the dynamical randomness of gases. While molecular chaos underlies the existence of gaseous thermodynamic states, this notion, and Boltzmann's
A signature of the nonlinear dynamics of fluids, and any dynamical system exhibiting deterministic chaos, is the divergence of initially close phase space trajectories. Finite-time Lyapunov exponents (FTLEs) are the exponential rates of divergence and important measures of the sensitivity to initial conditions characteristic of chaos. While their fluctuations on finite-time scales ultimately decay in the long-time limit, it is unknown how these fluctuations scale in the thermodynamic limit for fluids. This fact is largely because FTLE calculations are limited to systems that are small or restricted to one or two spatial dimensions. By overcoming this challenge, we have shown that the finite-size scaling of these fluctuations, that is, how they "self-average," is a quantitative representation of the van der Waals picture.
Thermodynamic states are generally a consequence of the self-averaging of microscopic properties. A system self-averages its independent subsystems if a global observable is an average of that observable over the independent subsystems. More precisely, a system is self-averaging with respect to a property if the relative variance decays to zero as the system size tends to infinity, with averages over statistical samples, independent subsystems, noise, disorder, or independent time windows. For equilibrium systems, the relative variance is of order 1/N but more generally can be Nγ, where γ is called the wandering exponent.
In this reporting period, we showed that the dominance of repulsive forces over attractive forces in the dynamics of fluids is manifest in the fluctuations of the Lyapunov spectrum. We showed the first Lyapunov exponent self-averages, but only weakly, for three-dimensional Hamiltonian models of simple fluids. Weak attractions merely act to slow the rate of decay of fluctuations scaling to the thermodynamic limit. The convergence of the fluctuations associated with the first Lyapunov exponent for the three-dimensional Hamiltonian systems here is distinct from the divergent behavior of the one-dimensional Hamiltonian models studied to date. We attributed this difference to the short-range interparticle forces in the WCA and LJ fluids. These forces affect the wandering exponent of the largest exponent but not the strongly self-averaging nature of the bulk exponents. Consequently, the fluctuations in the KS entropy diverge as one expects for an extensive thermodynamic quantity.
From the wandering exponents, the bulk Lyapunov vectors of Lennard-Jones and Weeks-Chandler-Andersen fluids belong to the same, as yet unknown, universality class. What is clear is that the classes of the first Lyapunov vectors are distinct. It remains to be seen whether the spatial dimension, the length scale of interparticle interactions, or both influences the rate at which fluctuations decay in the bulk of the spectrum. Still, it is tempting to speculate that increasing the length scale of attractive forces would further slow the convergence and, eventually, even cause fluctuations to diverge. Regardless of intermolecular forces, for simple equilibrium liquids, we also found evidence that the spontaneous fluctuations of these dynamical observables obey fluctuation-dissipation like relationships. Altogether, our results give an alternate view of the van der Waals picture of liquids, a view that opens up the possibility of examining emergent dynamical signatures at the liquid-gas critical point, in viscous liquids, or in self-organizing systems, where we anticipate long-range correlations to cause nontrivial self-averaging behavior.