62nd Annual Report on Research 2017

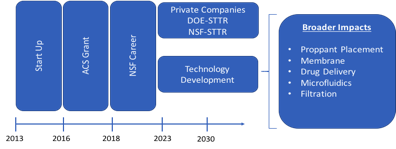
Career Development Plan: The PI’s CAREER plan and the long-term outcome of the project is shown in Figure 1. Development of a new theory to explain non-equilibrium (NE) effects in Particle-Particle-Fluid-Fluid (PPFF) flow systems is the PI’s long-term goal. The proposed theory will characterize and evaluate NE effects because of Fluid-Fluid (FF), Particle-Fluid (PF), and Particle-Particle (PP) phenomena, separately as well as collectively. Lack of knowledge to evaluate NE effects in the presence of a second immiscible fluid in the system and PP interactions are the main issues that the PI is facing in his current research activity.

The existing literature about NE in particulate systems has addressed only one phenomenon and the other phenomena either do not exist or, if they exist, their characteristic time are very short such that the equilibrium can be instantaneously attained. However, in many applications two or more phenomena can simultaneously exist and play role such as: low-salinity water injection, fines migration in oil reservoirs, membrane, environmental, and biomedical applications.:

Eq. 1

The validation of the proposed general theory will lead to several technology improvements (Figure 1).

Figure 1. Career Plan

Non-Equilibrium Effects: The notion of NE thermodynamics in transport phenomena has been explained in detail in [1]. In practice, many industrial and living systems that deal with transport of matter and of energy realize NE effects because of the interferences among complex sub-scale features in the system. Thus, inclusion of NE provides much accurate transport predictions for systems with significant gradients in velocity, pressure, and concentrations [2-15].

Non-Equilibrium Effects in Fluid-Fluid Systems: Capillary pressure plays an important role in evolution of FF interface and is a function of interfacial tension, wettability of solid surfaces, and microscale heterogeneities. Many studies have shown that local redistribution of fluids and creation of a stable interface between fluids in pores requires some time (relaxation time); the relaxation time may vary from fraction of a seconds to several hours [16-17]. NE effects can be significant whenever local gradients of dependent variables (fluids pressure and velocities) are not negligible. Several models have been proposed to describe NE effects of FF phenomena [18-22] and have been experimentally verified [23-28].

Capillary rise can be approximated by Washburn equation [29] that has been studied in recent years to analyze NE effects in small tubes [31-33]. Similar to Washburn equation for single tube/channel, several models have been proposed to describe dynamic capillary pressure in porous media [34-36] and have been experimentally verified [24-27]. For mathematical modeling of NE effects, a linear relaxation equation has been proposed [38]. The relaxation time in porous media represents time needed to establish equilibrium local saturations. The difference between dynamic capillary pressure and static capillary pressure represents local NE effects of FF phenomena. Previous studies have addressed NE effects of FF phenomena in porous media in Darcy-scale [22], experimentally [23-26], and pore-scale modeling [37-38].

The traditional approach of modeling NE is based on the linear relaxation time. However, consistent with some earlier reports in [39] and [40], the ACS results suggest that the first order relaxation time often fails to capture complex NE behavior. That is why, we will fundamentally investigate NE effects in particulate systems using a novel and integrated approach starting from simple channel system to more sophisticated systems.

Non-Equilibrium Effects in Particle-Fluid Systems: Modelling of particle transport has received extensive attention due to its importance in several scientific and industrial applications, such as proppant transport [41-42], deposition in the nasal and lung airways [43], environmental applications, pollutant transport, fluidized bed, and fuel spray in combustion engines [44-48]. Moreover, many researchers including the PI’s former student [49] have shown that the proppant transport (small solid particle) significantly affects the well productivity in shale plays [50-55]. Previous studies have shown that effect of NE in particulate transport can have significant consequences when relaxation time (velocity response time) is comparable to the characteristic time associated with the flow field [54-60].

Some Examples

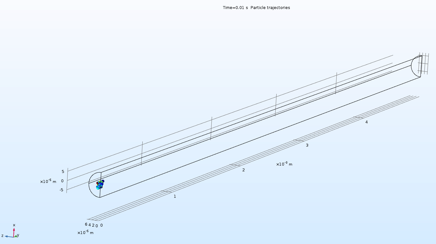
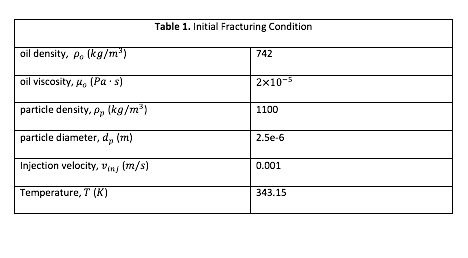
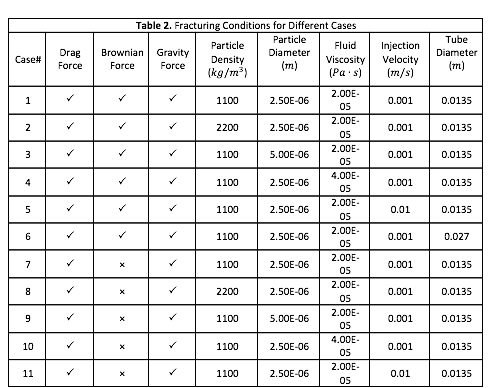
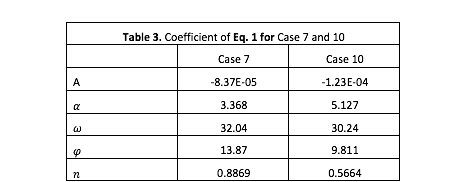
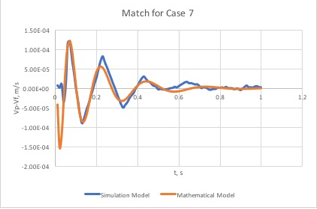
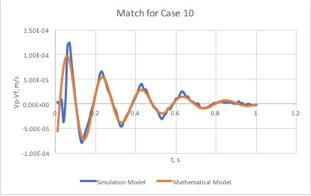
In this study, we use COMSOL, Mulitiphysics software to verify the accuracy of the proposed mathematical equation (Eq. 1) to explain NE in simple channel geometry (Figure 2). We consider three possible forces acting on particles during transport: gravity, viscous, and Brownian. Table 1 and Table 2 detail the simulation parameters. We validated the Task 1 of the proposed research on NE in channels. As it shown in Figures 5 and 6, a reasonable match was achieved between predicted values using Eq. 1 and the simulation results.

Figure 2. Transport Model for semi-cylinder system with spherical particles.

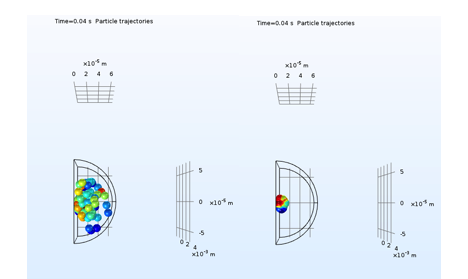
Figure 3. Particle trajectories with Brownian force at t=0.04s (left), and without Brownian force at t=0.04s (right)

Figure 4. Particle trajectories with Brownian force at t=1s (Top), and without Brownian force at t=1s (Bottom)

Figure 5. Predicted vs. simulation results for Case 7

Figure 6. Predicted vs. simulation results for Case 10