62nd Annual Report on Research 2017

Objective and Significance

Failures due to stress corrosion cracking (SCC) happen very often in the petroleum industry resulting in environmental risks and major economical expenses. Complex multiphysics and multiscale phenomena occurring in SCC have been the major drawbacks in understating, predicting and controlling SCC. Despite several years of intensive research, SCC is still not fully understood, and developing reliable physics-based models is needed to predict SCC. The goal of this project is to first develop an advanced phase field model coupled with atomistic simulations to predict oxidation nano and microstructures in metals, and then modify the framework to study SCC in steels.

Developing a Multiphase Field Model for Oxidation

A multiphase field model for oxidation of metals is being developed which consists of free energy equations that are functions of non-conserved structural order parameters for different phases, and conserved order parameters for different elements which needs to be tracked for the simulation. The total free energy will be the sum of an elastic term contribution and a chemical bulk free energy.

The governing equations used to control the evolution of the system are the Ginzburg-Landau equation for the non-conserved order parameters and the Cahn-Hilliard equation for the conserved order parameters. The evolution of stresses and strains is controlled using the mechanical equilibrium equation.

Results of Phase-Field Model of Oxidation

A model was created for FeO system, and the actual thermodynamic and physical properties of phases were used. Results in Figure 1 are based on considering composition (molar fraction) as the conserved parameter in the Cahn-Hilliard equation. Although results agree with the compositions of O and Fe in the air and FeO phases, considering molar fraction as the conserved parameter is not suitable for modeling the realistic problem. We are working to make the phase-field model in terms of concentration (instead of molar fraction) to make the model suitable to account for the gas-solid interactions.

The multiphase field model including several other phases of oxides will be developed. This model will include concentration parameters for each oxidizing element (Fe, Mn, Si, O), and one non-conserved order parameter for each phase (Fe, one for each oxide, and one for air). We will continue on improving the oxide model by making polycrystalline systems by adding grain boundaries, and we will optimize the computational efficiency until more material properties are available for the multiphase oxidation model.

Figure 1. Formation of oxide phase (FeO) in a 12nm×24nm domain during time (on the left). h parameters show the formation of phases (when the value is close to 1), and c parameters show the molar fraction of the corresponding element.

Development of Interatomic Potential for Fe-O System and Molecular Synamics Simulations of Oxidation

We have developed an interatomic potential for Fe-O system which consists of modified embedded-atom method (MEAM) and charge equilibration (Qeq) method, and describes the short range and long range interactions between atoms, respectively.

Initially, some properties of FeO were fitted based on NaCl (B1) structure. Values close to target values were obtained for cohesive energy, lattice constants and bulk modulus. However, the structure was not stable after minimization, or the atoms huddled together when we used “fix box/relax iso 0.0” to control the pressure. So those parameters, although resulted in very good predications of properties, were not appropriately creating the expected structure.

As the most stable structure of iron oxides is α-Fe2O3, we realized that it was not enough to just fit the properties of FeO to obtain the parameters. We calculated the cohesive energy and elastic constants of α-Fe2O3, which were not good enough. A lot of calculations were completed, and the MEAM and Qeq parameters were obtained.

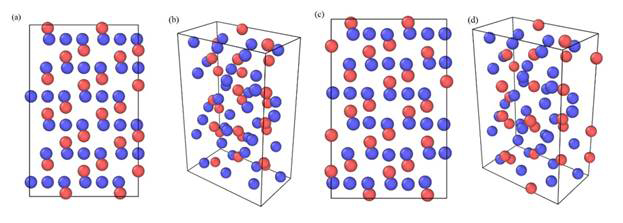
Since we did not modify any of the MEAM parameters for pure elements in MEAM library, our potential can be used directly for pure iron and oxygen elements without any modification. With these parameters we obtained the values of cohesive energy, lattice constants and elastic constants for both α-Fe2O3 and FeO, which are shown in Table 1. As shown in Figure 2, the structure of α-Fe2O3 is very stable after minimization and still stable at around 300 K with NVE ensemble after relaxation.

Table 1. The fitted and target values of cohesive energy, lattice constant elastic constants, and cation charge fora -Fe2O3 and FeO.

Figure 2. The structures of a -Fe2O3, (a) and (b) initial structure, (c) and (d) after minimization, in which red and blue particles represent Fe and O atoms, respectively.

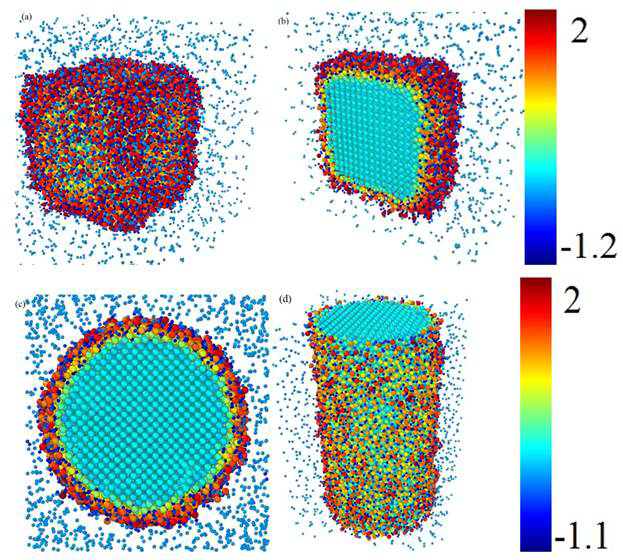
The kinetics of oxide growth on Fe surfaces are presented in Figure 3. Here, the color represents the charge state. It is shown that the O atoms are attracted to Fe surface and form Fe oxide on the Fe surface. In conclusion, the process of Fe oxidation can be well simulated based on the potential that we developed.

Figure 3. Snapshots of molecular dynamics simulation for oxidation reaction of (a) and (b) Fe nanoparticle and (c) and (d) Fe nanowire. Colorbar shows the charge.