62nd Annual Report on Research 2017

My research efforts related to flow through porous media comprise two main components: 1) experimentation and physical observations using microfluidics, and 2) modeling and numerical simulation.

Experimental Work

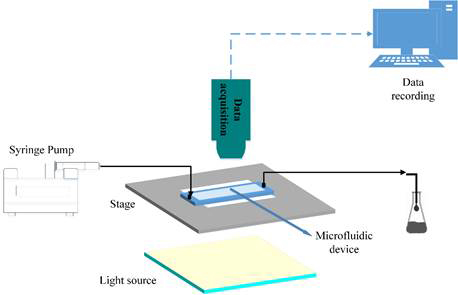
The microfluidics lab is leveraged to collect data regarding flow behavior and delineation between flow regimes as a function of capillary number and viscosity ratio for two immiscible phases. Figure 1 shows a schematic of the experimental set up.

Figure 1. Experimental setup.

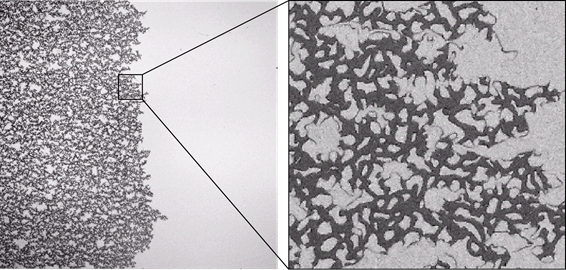
Data is captured in the form of high-resolution images, which are processed and analyzed. Examples of collected images are shown in Figs. 2 and 3. The observations are used to augment the delineation between various flow regimes reported in literature [1,2]. Length of the mixing zone and its evolution with time are also compared with related theory [3]. Once complete, the results of this work will be disseminated via a journal article and conference presentations.

In addition, the microfluidics capability was used to quantify the incremental oil recovery, as part of an EOR process, resulting from the use of environmentally friendly nanoparticles (by-product fly ash and recyclable iron oxide). These nanoparticles were shown to be effective in stabilizing CO₂ foam and in improving recovery in a microfluidic device saturated with crude oil. One journal article resulted from this work.

Furthermore, a heterogeneous microfluidic device was fabricated featuring one low permeability and two high permeability zones. The observations show that, in heterogeneous porous media, capillary entry pressure, in conjunction with apparent foam viscosity, is responsible for mobility control effects of foam and the resulting improved sweep efficiency. The observed displacement dynamics are explained by characterizing channel geometries and calculating capillary entry pressure values for various fluids and zones of the medium. A manuscript, detailing the experiments and the findings, has been submitted for publication and is currently under review.

;

Figure 2. Flow behavior as a function of capillary number and viscosity ratio.

Figure 3. An example of a high-resolution image.

Mathematical Modeling and Numerical Simulation

Currently, macroscale models, which are indispensable for simulating flow through porous media in large-scale systems, often suffer from lack of predictive capabilities due to flow instabilities [4]. Despite the development of alternate constitutive relations, competing models do not show significant improvements in their predictive capacity for large-scale systems, and they lead to stability issues and prohibitive computational costs in numerical simulation. This was shown through comparison of experimental data with simulation results using classical and nonequilibrium models for flow through porous media. The results were published in a journal article.

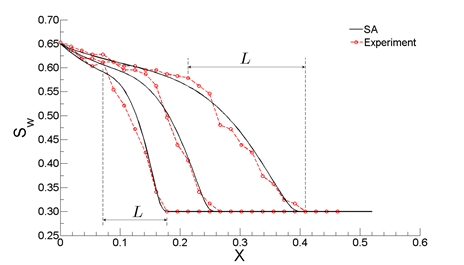
Experimental results are used to guide the development of a robust, self-consistent and physics-based macroscale formulation for multiphase flow in porous media. Preliminary results (Fig. 4) suggest that multiscale homogenization of the conservation of momentum will finally close the gap between experimental observations and numerical results of macroscale models. The working hypothesis is that the inconsistent length scales associated with the extension of Darcy’s law from single to multiphase flow is responsible for the lack of predictive capabilities of macroscale models. The mathematical model is guided and verified by experimental data collected in the lab. Two manuscripts, based on the mathematical modeling and numerical simulation efforts, are currently in preparation.

Figure 4. Comparison of three saturation profiles from a core-scale displacement experiment (cross-sectional average), with a viscosity ratio (invading to resident) of 20, adapted from [5] (“Experiment”), and numerical solutions obtained using the proposed model (“SA”) (preliminary results).

Impact on Career and Student Development

The ACS-PRF grant has been instrumental to my career development. It has enabled me and my graduate students to undertake fundamental research related to flow instabilities in multiphase flow in porous media. With the support I received from ACS, we have conducted flow experiments using microfluidics and collected data, which I am leveraging in new proposals to various state and federal agencies. The publications that have resulted from this work, and will result in the coming year, play an important role in establishing a track record that will help in my future research projects.

References:

1.      R Lenormand. Liquids in porous media. Journal of Physics: Condensed Matter, 2:SA79, 1990.

2.      C Zhang, M Oostrom, TW Wietsma, JW Grate, and MG Warner. Influence of viscous and capillary forces on immiscible fluid displacement: Pore-scale experimental study in a water-wet micromodel demonstrating viscous and capillary fingering. Energy & Fuels, 25(8):3493–3505, 2011.

3.      GI Barenblatt, TW Patzek, and DB Silin. The mathematical model of nonequilibrium effects in water-oil displacement. SPE Journal, 8(4):409–416, 2003.

4.      A Riaz, GQ Tang, HA Tchelepi, and AR Kovscek. Forced imbibition in natural porous media: Comparison between experiments and continuum models. Physical Review E, 75(3):36305, 2007.

5.      GQ Tang and AR Kovscek. High resolution imaging of unstable, forced imbibition in Berea sandstone. Transport in porous media, 86(2):647–664, 2011.