62nd Annual Report on Research 2017

The goal of this project is to establish methods for homogenizing suspensions of hard particles in extremely viscous liquids. Our results will allow improved handling of particle and fiber suspensions, such as viscous bitumen and drilling fluids. With the support of the American Chemical Society Petroleum Research Fund (PRF) over the last year (Aug. 1, 2016 to Aug. 31, 2017), we have made significant progress towards this goal. Below, I summarize key results during this funding period in three thrusts of the project. Finally, I summarize the impact of this funding on my students and my scientific career.

(1) Self-organized hyperuniformity.– The primary effort in this funding year has been on studying a model of cyclically-sheared viscous suspensions through computer simulations and analytical arguments. We are using this model to test protocols for obtaining extremely homogenous distributions of particles in a viscous liquid, thus providing a new handle for controlling extremely viscous suspensions that are hard to mix by conventional methods.

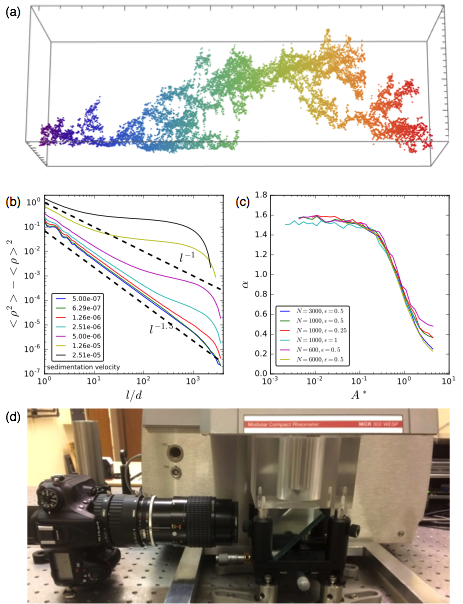
The simulation model, originally developed by Laurent Corté and coworkers, has been shown to capture the essential aspects of such viscous suspensions, through work performed by myself and others in recent years. The model simulates the irreversible displacements of N particles of diameter d at packing fraction φ, driven from the boundaries by cyclic shear. Slow particle sedimentation at velocity v can also be added. To test our implementation of the algorithm, we looked at space-time clusters in our simulations, as has been done before. Figure 1(a) shows an example of such a cluster in our simulations. The horizontal axis and color denote increasing time (left to right and purple to red); the perpendicular plane indicates the position of colliding particles in 2D space. By measuring the distribution of sizes of such clusters, we demonstrated that we see criticality in our simulations.

Next, we measured the degree of homogenization in our systems for different system sizes, sedimentation speeds, diffusion constants, and shear amplitudes, in both one-dimensional (1D) and 2D versions of the model. Figure 1(b) shows our measurements of fluctuations in area fraction in the 1D system as a function of the lengthscale, l, over which area fraction is measured. The scaling exponent, α, indicates the quality of dispersal; higher α corresponds to a faster decay of fluctuations and thus a higher degree of homogenization. These simulations confirmed our main hypothesis: at low sedimentation velocity, we achieve a high quality of dispersal.

Figure 1(c) shows that all our measurements of the scaling exponent, α, can be collapsed onto a master curve when plotted as a function of a newly-discovered parameter, A*=Nvd/2φ_cD, where φ_c is the critical packing fraction for the irreversibility transition and D is the diffusion constant in the irreversible phase. Thus, we have identified a quantitative criterion for homogenizing suspensions of sedimenting particles by applying cyclic shear. This work is currently being written up for publication.

(2) Experiments.– We have also made progress constructing an apparatus for testing this protocol in experiments. We have produced suspensions made of 125-micron PMMA spheres in a ternary mixture of water, zinc chloride, and Triton X-100 to match the index of refraction of the particles. We also built a custom shear cell and imaging system around a strain-controlled rheometer that we installed in the lab. A photo of the experimental setup is shown in Fig. 1(d). In the next year, we will carry out experiments to test the shear protocols from the simulations.

(3) Rate of relaxation.– Understanding the timescales for relaxation to a steady state is important for throughput in applications. These timescales are also interesting from a fundamental perspective: One wants to know how non-equilibrium systems composed of large particles (such as foams, suspensions, and granular materials) approach steady-states under cyclic driving. We conducted numerical simulations to investigate the time-dependence of the self-organization process. Simulations of the 2D model show a stretched-exponential form, which is characteristic of glassy systems. Remarkably, this same functional form was maintained even in a 1D version of the model that is completely deterministic, where the only randomness is in the initial particle positions.

To understand this behavior, we decomposed the problem into clusters of particles that act independently of each other throughout the relaxation. We discovered an analytical expression for the distribution of cluster sizes, by mapping the problem to a first-passage time for a Brownian bridge. We also found that the relaxation in a cluster depends only on its size. We were thus able to reconstruct the total relaxation of the full system, and show that it has a functional form that is well-approximated by a stretched exponential. These results were published in the current funding year, in the Journal of Statistical Physics.

Impact on my students and my career.– This grant provided support for one graduate student, Jikai Wang, during the entire reporting period. Through this support, Jikai learned to write numerical simulations and analyze the results, which he presented at the 2017 APS March Meeting in New Orleans. Jikai will continue to be supported on this grant in the coming year. The grant also supported a summer intern, Arthur Hernandez, prior to his first year in the Physics graduate program at Syracuse University. Arthur helped construct the experimental apparatus. (He is now working on soft matter theory with a colleague in the department.) These funds continue to support the purchase of materials and lab supplies for the experiments, and they provided a portion of my summer salary. Finally, this was my first research grant, and it greatly helped me in establishing my independent research program.